Задача 47-4. Лежачий камень

Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов

А.

Корчуя садовый участок, мы обнаружили большущий камень. Как и следовало ожидать, он лежал как раз там, где не следовало. Естественно, его нужно было убрать, и мы приступили. Камень был далеко не круглым, поэтому кантовать его было трудно, хотя путь, по которому мы его катили, был достаточно ровным. Мы дружно кричали «раз – два, взяли!» – и камень, поднявшись на попа, затем шлепался вперед.

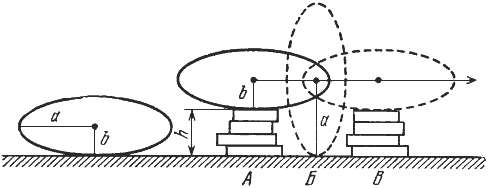
Рис. 51. Кантуем элиптический камень

– Стой, ребята, не так! – закричал Гена Иванов, наш сосед. Он быстро набросал впереди камня горку обрезков досок (рис. 51, А) и вместе с нами налег на камень. Тот легко перевалил через доски. Приказав нам держать его вертикально (Б), Гена перенес горку обрезков опять вперед камня (В) и последний опять сам, почти без нашей помощи, форсировал это препятствие*. Это было как в сказке: по ровной дороге камень катиться не желал, а по ухабам – с удовольствием!

* Автор признателен Г.Ф. Иванову за помощь в транспортировке камня и за демонстрацию эффектного приема, подсказавшего эту задачу.

Почему неровная дорога лучше ровной? Каковы принципы конструирования наилучшей дороги для камней разного сечения? Всякому ли камню можно приготовить идеальную дорогу?

Б.

Начнем с шарообразного камня. Очевидно, для него наилучшая дорога – гладкая и горизонтальная. А если она к тому же еще и твердая, то шар массой в тонну можно катить по ней одним пальчиком. То же верно и для цилиндрического камня с круглым сечением. Почему, если сечение камня не круглое, то трудности существенно возрастают?

В.

Шарообразный камень по гладкой горизонтальной твердой дороге катится почти без усилий: в силу шаровой симметрии его центр масс движется равномерно и прямолинейно, параллельно дороге и, следовательно, горизонтально и поэтому в принципе никаких затрат энергии не требует. На практике энергия нужна для преодоления трения и – вначале – для придания камню поступательного и вращательного движения, а в конце – для остановки (если не поручить это трению).

Камень любого другого сечения, очевидно, требует дополнительной работы по поднятию его центра масс при переходе из «лежачего» в «стоячее» состояние. Затем эта работа бездарно растрачивается при падении «стоячего» камня, после чего его вновь требуется поднимать и т.д. Очевидно, вся сила рационализаторского предложения Гены в том, чтобы, раз поставив камень «на попа», в дальнейшем не растрачивать всей его потенциальной энергии на падение, а делать подставку такой высоты, при которой изменение высоты центра масс при переходе камня из вертикального положения в горизонтальное было бы минимальным. Очевидно, что для эллиптического камня высота подставки должна равняться h = a – b, где a и b – большая и малая полуоси эллиптического сечения камня (рис. 51). Тогда в обоих положениях центр масс камня будет на одной высоте, Т.е. такое качение эллиптического камня по «ухабам» почти эквивалентно качению шарового камня по горизонтальной плоскости.

А почему «почти»? А потому, что, кроме вертикального и горизонтального, у камня есть и промежуточные, наклонные положения. Нельзя ли сконструировать такие «ухабы», чтобы камень эллиптического, квадратного или треугольного сечения катился по ним так же легко, как шар по плоскости?

Сознаемся сразу: нам не удалось найти строгое решение задачи. По правилам игры такую задачу не следовало бы включать в книгу, так как она бросает тень на умение автора всегда смотреть в корень. Но шут с ней, с тенью! Уж больно интересная задача. К тому же, как вы видели, практически ценная. И не только для перекатывания камней. Она наверняка пригодилась бы в теории механизмов. Да мало ли где! Часто задача, решенная в одной области, вдруг находит применение в другой, казалось бы, очень отдаленной. Так, энтропия термодинамики вдруг заработала в теории информации. Пути науки неисповедимы. В науке поставить задачу иногда важнее, чем ее решить.

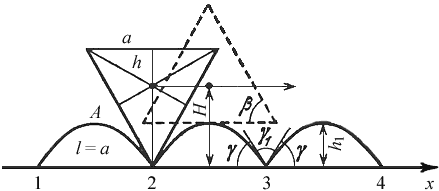
Рис. 52. Перекатывание трехгранной призмы

Начнем с камня-призмы с сечением в виде правильного треугольника со сторонами a (рис. 52). Центр масс треугольника – на пересечении его медиан (и, для данного треугольника, биссектрис и высот), на расстоянии h/3 от любого из оснований. Поскольку h = a√[3/2] и h/3 = a/2√[3], то для постоянства высоты H центра масс (H = a/√[3]) при качении высота дороги должна меняться в пределах от 0 до h₁ = a/2√[3]. Длина кривой «ухаба» 1-A-2 должна равняться l = a; если равенство не соблюдено, то треугольник, катясь стороной a по l, станет на свою вершину не в углублении, а ближе него или дальше, отчего он поднимется, и будет нарушено главное требование H = const. Правда, можно допустить l ≠ a, если допустить скольжение по ухабу. Но каждый, кому приходилось заставлять тяжелый камень «скользить» по земле, асфальту или другому камню, скажет, что лучше уж нарушить требование H = const, чем мучиться со скольжением.

Что еще можно сказать о кривой 1-A-2 с первого взгляда? Нужно потребовать, чтобы в точках 1, 2, 3 она подходила к оси абсцисс под углом γ = 60°. Если γ > 60°, то вершина камня (β = 60°) просто не войдет в углубление, камень зависнет. Если же γ < 60°, то γ₁ > 60° = β, и камень не сможет стоять в углублении на своей вершине: он будет валиться набок, что равносильно вращению камня вокруг точки 2 (или 3) и нарушению H = const.

И этот же угол γ₁ должен быть ≥ 90°, иначе камень, вылезая из впадины, обломает либо свою вершину, либо предыдущий ухаб, который он уже, казалось бы, преодолел. Противоречивость требований к углу (γ₁ = 60° и γ₁ ≥ 90°) означает, что для камня типа треугольной призмы оптимального (в смысле H = const) профиля дороги не существует.

Конечно, можно каждый раз, остановив камень «на голове», перенести ухаб сзади наперед и т.д. Но эта беготня не украсит решение задачи.

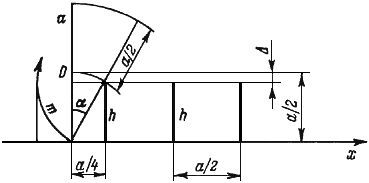
Рис. 53. Перекатывание пластины

Отсюда же следует, что невозможно строго решить задачу и для камня в виде бесконечно тонкой пластины, потому что ее сечение можно рассматривать как предельный случай треугольника, у которого один из углов стремится к нулю. Для пластины лучшее из того, что удалось построить, показано на рис. 53. Стоящую вертикально пластину длиной a нужно наклонять вправо, пока ее центр масс O не сместится вправо на x = a/4. Подставив под ее центр масс подставку высотой h, будем вращать пластину вокруг вершины подставки как центра. Левый конец ее, описав дугу m, укажет пространство, в котором запрещено пребывание предыдущего ухаба. Итак, шаг между подставками должен быть a/2. Центр масс пластины не движется горизонтально, он то опускается на Δ = a/2 – h, то поднимается.

Величина h = (a/2)·cos α, α = 30°, тогда

Δ = (a/2)(1 – cos α) = (a/4)(2 – √[3]) ≈ 0,07a,

т.е. примерно одна седьмая от того перемещения a/2, которое было бы при «перекатывании» пластины по гладкой дороге*.

* А если учесть, что по гладкой дороге камень при перевороте продвигается вперед на a, а по нашей – только на a/2, то результат оказывается вдвое хуже.

Квадратное сечение не дает в углублении тех хлопот, которые были с треугольным. Но только квадратное: прямоугольник в общем случае не удастся выкатить из углубления. Правильные пяти-, шестиугольники (и т.д.) тоже выкатываются из углубления без разрушений. И чем многоугольнее n-угольник, тем ближе строгое решение: в пределе, при n → ∞, мы имеем круглое сечение, идеал всех камней и дорог.

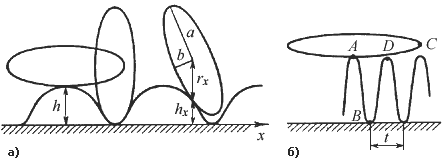
Рис. 54. Перекатывание эллипса: а) обычного; б) при малом b

Казалось бы, эллиптическое сечение не доставит хлопот (рис. 54, а): строй высоту профиля дороги h_x такой, чтобы в паре с соответствующим «радиусом» эллипса r_x она составляла нужную высоту H = h_x + r_x = const – и вся недолгá. Тем более, что одной из крайностей для эллипса является окружность (b = a), для которой все ясно. Но вспомним другую крайность. Представим эллипс с b → 0. И мы вернемся к бесконечно тонкой пластине (рис. 53). Как же ведет себя эллипс в остальных случаях? Плохо, и в этом можно легко убедиться при малом b (рис. 54, б). Требование качения без скольжения сводится к равенству длин соприкасающихся линий. В нашем случае нужно, чтобы AB = l/4, где l – периметр эллипса. При малых b имеем AB ≈ l/4a. Как видно из рисунка, при этом ухабы получаются весьма изрезанными и шаг их меньше a, отчего эллипс в положении лежа простирается сразу над несколькими ухабами и не может закатиться в углубление. Чем меньше b, тем гуще ухабы, и в пределе при b → 0 шаг ухабов t → 0.

По мере увеличения b эта трудность должна уменьшаться; на рис. 54, a она уже перестала быть очевидной. Но при непрерывном увеличении b она не может исчезнуть скачком: точка D, в которой ухаб препятствует вращению камня, по мере увеличения b будет перемещаться по эллипсу к вершине C, а по ухабу – к впадине B. Препятствие, по-видимому, исчезнет только при b = a, когда эллипс превратится в окружность. Строгое доказательство этого требует применения дифференциальной геометрии, которая вне рамок данной книги. Вполне возможно, что кем-то где-то эта задача уже решена, но найти в литературе это решение не удалось.

Если кто-то из читателей захочет вывести автора из положения барона фон Гринвальдуса, то для него формулируем основные свойства нужного рельефа дороги. В каждой точке дороги равновесие камня должно быть безразличным, как равновесие шара на горизонтальной плоскости. Это требование геометрии и статики. Ухабы не должны заклинивать камень, лишая его возможности передвигаться. Это требование геометрии и кинематики. Требование динамики: катящийся камень должен иметь равномерные поступательное и вращательное движения, или, поскольку это требование, по-видимому, невыполнимо, то по крайней мере кинетическая энергия суммы этих движений должна быть постоянной. Так это у шара на горизонтальной плоскости, и этого же мы хотим от нашего камня на ухабах. Для начала можно пренебречь требованиями динамики. Если строгого решения нет, неплохо найти наилучшее из возможных. Вашему воображению поможет картонная модель сечений камня и дороги, положенная на стол.

Неужели нельзя превзойти решение Гены?

• Задача 48. Да будет свет!

• Оглавление

Дата публикации:

4 сентября 2003 года