Задача 54. Пловцы и волны

Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов

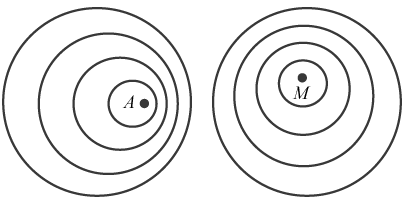
А.

Перед вами «снимок» глади озера сверху (рис. 69). Точки – пловцы, окружности – волны. Куда плывут пловцы? Какой из пловцов плывет быстрее? Какова скорость пловцов, если скорость волн 0,5 м/с?

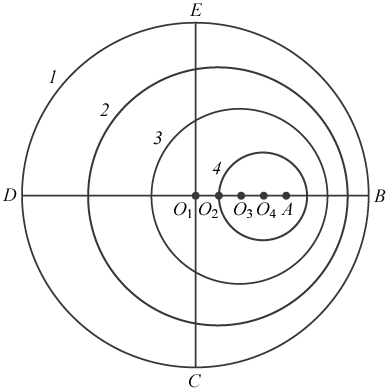
Рис. 69. Схема расположения пловцов и волн

Б.

Найдите точки, в которых находились пловцы в начале заплыва. Стоп! Дальше не читать! Подумайте!

Если ничего не придумали, читайте дальше. Скорость волны одинакова по всем направлениям; Поэтому волна и является окружностью: от той точки, где она возникла (центра окружности), она прошла по всем направлениям одинаковое расстояние. Очевидно, самая первая волна успела продвинуться дальше всех. Значит, это окружность наибольшего радиуса. Центр этой окружности и есть место старта пловца. Теперь вы без труда ответите на поставленные вопросы.

В.

Каждая волна создается пловцом. Очевидно, центры всех окружностей изображают последовательные положения пловца. Центр самой большой окружности O₁ (рис. 70) изображает первоначальное положение пловца. Следовательно, пловец A плывет вправо, пловец M – вперед (на чертеже – вверх). За время, за которое пловец проплыл из точки O₁ в A, волна 1 прошла расстояние O₁B = O₁C = O₁D = O₁E. Расстояние O₁B, как следует из измерений по рисунку, вдвое больше расстояния O₁A. Следовательно, скорость пловца A вдвое меньше скорости волны, т.е. равна 0,25 м/с. Аналогично измеряем скорость пловца M. Она еще меньше – 0,125 м/с.

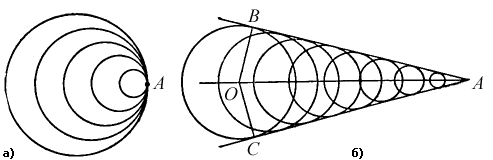
Рис. 70. Определение первоначального положения пловца

Оценим теперь качественно картину волн в зависимости от скорости пловца. Если пловец барахтается на месте, он создает концентрические кольца волн. Если он движется, то волны сгущаются в том направлении, куда он плывет, и разрежаются в противоположном направлении. Сгущение тем сильнее, чем больше скорость пловца. Так будет до тех пор, пока скорость пловца не сравняется со скоростью волн. Тогда все окружности – большие и малые – касаются друг друга в одной точке, а именно в той, в которой находится пловец (рис. 71, а). Если пловец движется быстрее волн, то картина оказывается сложнее (рис. 71, б). Наиболее отчетливо в ней виден клин из двух прямых волн AB и AC – общих касательных ко всем круговым волнам. Внутри же клина картина очень запутана: здесь в отдельных местах гребень одной волны складывается с гребнем другой и получается более высокий гребень, в других же местах складываются две впадины, в третьих – гребень одной с впадиной другой. И только на прямых AB и AC мы имеем простую картину: вдоль этих прямых выстроились гребни всех кольцевых волн.

Рис. 71. Определение места нахождения пловца

Построив точку старта O и соединив ее с A и B, мы получаем прямоугольный треугольник OAB, у которого гипотенуза OA изображает путь, пройденный пловцом, а катет OB – путь, пройденный волной за то же время t. Если обозначить угол BAC буквой α, то OB/OA = sin (α/2). Разделив числитель и знаменатель левой части на t, мы получаем слева отношение скоростей волны v_в и пловца v_п. Таким образом, скорость пловца можно найти по формуле

v_п = v_в / sin (α/2).

Чем острее клин (меньше α), тем больше скорость пловца.

Отметим, что аналогичный клин звуковых волн создается у самолета, летящего со скоростью, большей скорости звуковых волн (со сверхзвуковой скоростью). Этот клин (точнее, поверхность конуса, поскольку в этом случае речь идет о движении волн в среде с тремя измерениями), набегая на наблюдателя, создает у него впечатление орудийного выстрела, после которого наблюдатель, находясь уже внутри конуса, начинает слышать обычный звук самолета.

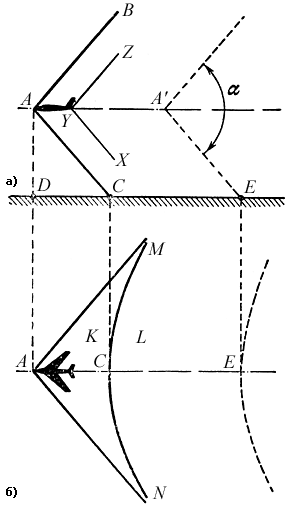
Рис. 72. Клин звуковой волны, создаваемый самолетом

Такой конус показан на рис. 72 (а – вид сбоку, б – вид сверху). На поверхности конуса давление выше, чем снаружи и внутри. Вблизи самолета перепад давления может достигать значительной величины, зависящей от высоты полета, типа машины, ее скорости; поэтому ударная волна низко летящего сверхзвукового самолета может произвести заметные разрушения. Но при высоте полета более 10 000 м волна достигает земли с давлением, превышающим атмосферное не более чем на доли процента.

Земной наблюдатель D видит самолет A в зените, но не слышит его звука; на наблюдателя C в данный момент набегает поверхность конуса с повышенным давлением, и он слышит «выстрел». Наблюдатель E находится внутри конуса, он слышал «выстрел» в момент, когда самолет находился в точке A', а сейчас слышит обычный гул самолета.

Часто удается различить, что «выстрел» двойной: второй удар происходит от хвостовой волны ΧΥΖ (на поверхности этого конуса давление ниже, чем снаружи и внутри).

Линия пересечения конуса и плоской поверхности земли – гипербола NCM, во всех точках которой «выстрел» слышен одновременно. Она отделяет зону K, в которой самолет еще не слышен, от зоны L, в которой он уже слышен. Эта гипербола движется по земле со скоростью самолета. Кстати, не поленитесь вычислить эту скорость, исходя из того, что на рисунке α = 100°.

Более подробно об этом явлении можно прочесть в брошюре: Миронов А.Д. Сверхзвуковой «хлопок» самолета. – М.: Воениздат, 1964.

Обратите внимание, что приведенная формула при v_п < v_в дает

sin (α/2) = v_в / v_п > 1,

что невозможно. Не надо думать, что это ставит под сомнение правильность формулы. Наоборот, своим экстравагантным поведением формула предостерегает читателя, чтобы он держал ухо востро: область применения формулы кончилась, при v_п < v_в картина волн меняется не только количественно, но и качественно, клин волн исчезает, угол α теряет физический смысл, картина волн становится подобной рис. 69.

• Задача 55. Волны и поплавки

• Оглавление

Дата публикации:

23 октября 2003 года