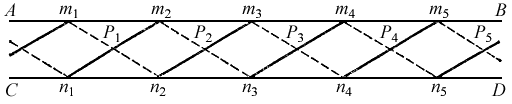
Задача 58-3. Катер мчится по каналу

Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов

А.

Допустим, что вы живете на берегу прямого канала с аккуратно облицованными стенками (в Ленинграде на Фонтанке, например). Вы выглянули в окно и видите, что вся гладь канала взбудоражена мечущимися между стенками волнами, сходящимися и расходящимися, образующими красивый живой узор. Основные волны этого узора показаны на рис. 70. Волны, показанные пунктиром, идут от стенки AB к стенке CD; волны, показанные сплошными прямыми, идут в обратном направлении. По-видимому, по каналу прошел катер. Попробуйте определить, в какую сторону он ушел, и какова была его скорость. Будем считать, что волны в воде канала распространяются со скоростью 1 м/с (на самом деле скорость различна для разных длин волн и поэтому картина несколько сложнее показанной на рисунке).

Рис. 70. Результирующая картина сложения волн

Б.

Решить эту задачу вам поможет ответ на задачу о пловцах и волнах. Из нее вы узнали, что от пловца или от катера, развивающего скорость больше скорости волн, расходятся клинообразно две четко выраженные волны, угол α между которыми позволяет определить скорость катера:

v_к = v_в / sin (α/2).

На рис. 71 показан катер и клин волн OA и OC. Если бы не было стенок, эти волны, очевидно, продолжались бы по пунктирным прямым AA' и CC', Нарисуйте их продолжение при наличии стенок. Закон отражения вам хорошо известен.

Рис. 71. Образование волнового фронта

В.

Рис. 72. Схема сложения волн

Пусть в данный момент нос катера находится в точке a (рис. 72), а одна из создаваемых им волн находится на прямой abcdefg. Через некоторое время t нос катера будет в точке a', а сопровождающая его волна займет положение a'a₁b₁c₁. Все точки волны движутся с одинаковой скоростью, направленной перпендикулярно к фронту волны. Поэтому за время t все они пройдут одинаковые расстояния aa₁, bb₁, cc₁. Точка d волны должна пройти такое же расстояние, но на своем пути в точке d₁ она встретит стенку и, отразившись от нее под углом отражения, равным углу падения (γ = β), пройдет дополнительно путь d₁d₂. Общий путь точки d за время t будет ломаным, длина же его будет равна длине пути любой другой точки волны:

dd₁d₂ = cc₁ = bb₁ = aa₁.

Аналогично отразятся и остальные точки волны, так что

ee₁e₂ = ff₁f₂ = gg₂ = aa₁.

В результате точки отраженной волны выйдут на прямую c₁d₂e₂f₂g₂, наклоненную к стенке под таким же углом α/2, под каким наклонена к ней падающая волна a'a₁b₁c₁.

Отраженная волна будет двигаться к противоположной стенке по направлению d₁d₂ (или e₁e₂, f₁f₂). Треугольники c₁d₁d₂ и c₁d₁d₃ подобны: d₃d₁ перпендикулярно к c₁d₁, a d₁d₂ перпендикулярно к c₁d₂, т.е. оба треугольника прямоугольны, второй же угол α/2 является для них общим; поэтому равны и третьи углы. Следовательно, α/2 = γ.

Отражение от противоположной стенки будет происходить аналогично. В результате многократных отражений канал на большом протяжении будет заполнен двумя сериями косых волн, проходящих друг сквозь друга без каких-либо помех.

Нетрудно видеть, что точка c₁, в которой происходит излом волны a'c₁g₂ при отражении, перемещается влево вдоль стенки канала со скоростью, равной скорости катера. В самом деле, если бы скорость точки c₁ была меньше скорости носа катера a', то точка c₁ все больше и больше отставала бы от катера, отчего прямая a'c₁ была бы все более горизонтальной (на чертеже), т.е. угол α/2 все время уменьшался бы. Но ведь

α/2 = arcsin (v_в / v_к),

т.е. зависит только от скорости катера v_к и скорости волн v_в, которые постоянны. Следовательно, постоянен и угол α/2, прямая a'c₁ будет перемещаться параллельно самой себе, что возможно, только если c₁ перемещается с такой же скоростью, как и a'.

Точно так же доказывается, что и остальные изломы волн у берегов (точки m₁, m₂, m₃, ..., n₁, n₂, n₃, ... на рис. 70) перемещаются со скоростью катера. Более того, точки p₁, p₂, p₃, ..., в которых волны пересекаются на середине канала, тоже движутся в ту же сторону и с той же скоростью. Следовательно, если вы действительно стоите на берегу канала и наблюдаете живую картину волн, а не неподвижный рис. 70, то для определения скорости прошедшего по каналу катера вам даже не обязательно знать скорость волн: вам достаточно определить скорость передвижения любой из точек m₁, m₂, n₁, p₁ и т.д. Вся картина волн мчится за катером с его скоростью, хотя каждая из волн, перемещаясь в направлении, перпендикулярном к своему фронту, движется довольно лениво.

В какую же сторону ушел катер на рис. 70? Волна n₁m₂, показанная сплошной прямой, идет к стенке AB, m₂n₃ – к стенке CD. Точка их стыка m₂ перемещается влево. Следовательно, и все остальные точки, а также и катер, перемещаются влево.

Скорость катера можно определить, измерив угол α, под которым пересекаются волны. Измерение дает α = 60°. Следовательно,

v_к = v_в / sin (α/2) = 1 / (sin 30°) = 2 м/с.

• Задача 59. Гром и молния

• Оглавление

Дата публикации:

15 декабря 2003 года