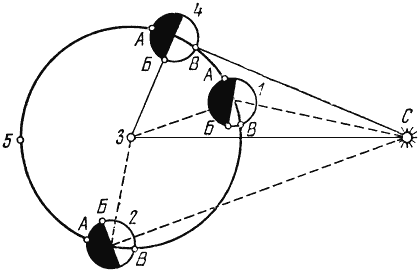
Задача 71. Даешь полумесяц!

Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов

А.

Представим, что лучшей половине человечества из непонятного (но обязательного для исполнения худшей половиной) каприза захотелось, чтобы Луна всегда была не слишком полной и не слишком серпом, а точно полумесяцем. Так сказать, не макси, не мини, а миди! Найдите геометрическое место точек в Солнечной системе, которые удовлетворяют этому капризу. Сумеете ли вы подобрать для Луны соответствующую орбиту?

Б.

Рассмотрите треугольник Солнце – Земля – Луна. Каким он должен быть, чтобы мы с Земли видели лунный диск освещенным ровно наполовину?

В.

Рис. 93 напоминает вам о том, как возникают различные фазы Луны. Размеры Луны и ее орбиты на рисунке сильно преувеличены по сравнению с Солнцем, Землей и расстоянием между ними ЗС. Это позволяет детально рассмотреть Луну и ее фазы и, кроме того, не считаться с эффектами параллакса, вызываемыми конечными размерами Солнца и Земли.

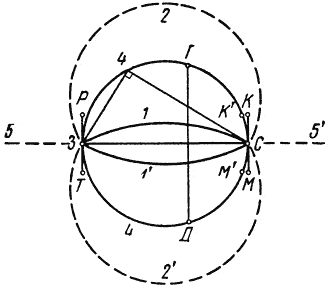
Рис. 93. Построение фаз Луны

В положении 1 (угол Земля – Луна – Солнце тупой) Земля видит бóльшую часть Луны АБ неосвещенной и меньшую БВ (серпик) – освещенной. В положении 2 (угол ЗЛС острый) – наоборот. В положении 4 (угол ЗЛС прямой!) АБ = БВ, т.е. мы видим полумесяц. Очевидно, прямой угол у Луны есть обязательное требование для фазы полумесяца.

Будем для простоты расстояние Земля – Солнце (ЗС) считать постоянным и прямую ЗС неподвижной. Найти геометрическое место вершин прямого угла, опирающегося на отрезок ЗС, легко: вспомним, что если вершина угла, опирающегося на диаметр, лежит на окружности, то этот угол – прямой. Значит, геометрическим местом положений Луны, дающих полумесяц, является окружность, построенная на отрезке ЗС как на диаметре (рис. 94). Переходя от плоского чертежа к трехмерному космосу, мы в качестве искомого геометрического места будем иметь шаровую поверхность, построенную на том же диаметре.

Геометрическое место точек для серпика (положение 7 на рис. 93) также находится на дуге окружности (1 на рис. 94), только большего радиуса, так как теперь отрезок ЗС должен быть хордой (искомый угол – тупой, а не прямой).

Любопытно, однако, что на продолжении дуги 1 (по другую сторону от точек З и С) будет не светлый, а темный серпик тех же размеров (фазы), т.е. светлая часть Луны будет не серпиком, а его дополнением до полной Луны. Если же требуется светлый серпик, то нужно построить дугу 1' того же радиуса, что и 1, но принадлежащую другой окружности. Итак, геометрическим местом серповидной Луны на плоскости является не окружность 1, а сочетание дуг 1 и 1'. В пространстве геометрическим местом будет поверхность типа веретена, образованная вращением дуги 1 вокруг прямой ЗС. Аналогично, черный серпик (ущербленная Луна) получается вращением дуги 2 вокруг той же прямой (при этом полученная поверхность напоминает поверхность яблока). Для полной Луны геометрическим местом точек являются две полупрямые: З5 и С5' (однако на первой из них Луна находится в тени Земли, на второй – спрятана от нас за Солнцем); для новолуния – отрезок ЗС.

Рис. 94. Не кеплеровы траектории луны

С геометрией покончено. Перейдем к физике (небесной механике). Задачу можно решить, остановив Луну (относительно Земли) в положении 4 (рис. 94). Но тогда она упадет на Землю. Добровольно по окружности 4 Луна не пойдет: траектория 4 явно не кеплерова (как и «веретено», и «яблоко»). Кроме того, даже если мы принудим ее к этому с помощью двигателей, то она после полуоборота все равно столкнется либо с Солнцем, либо с Землей.

Но нам вовсе не обязательно держать Луну в плоскости чертежа. Ведь геометрическим местом точек для полумесяца является сфера 4. Если бы Луна двигалась по окружности, перпендикулярной прямой ЗС (например, в плоскости ГД), то фаза ее была бы постоянной (полумесяц – на сфере 4, серп – на веретене 1 и т.д.). Но эта траектория тоже не кеплерова: у кеплеровой центр притяжения (либо Солнце, либо Земля) должен находиться в плоскости орбиты. Задание будет «почти выполнено», если Луну заставить вращаться вокруг Солнца в плоскости КМ. Поскольку точки К и М мало отличаются от нужных К' и М', то и фаза Луны будет мало отличаться от полумесяца. Авось заказчик не заметит разницы! Тем более что теперь Луна будет видна с Земли лишь как очень яркая точка, а проверить правильность выполнения задания можно только через телескоп. Кроме трудностей перевода Луны на эту орбиту здесь есть и другие: плоскость должна быть всегда перпендикулярна прямой ЗС, которая, как известно, поворачивается. Итак, придется еще заставить плоскость КМ совершать один оборот в год вокруг оси КМ.

После всех этих фантастических трудностей орбита в плоскости РТ (содержащей Землю) кажется почти реальной (хотя плоскость РТ тоже нужно поворачивать, как и КМ). Еще ближе к реализуемости проект, в котором используется не сама Луна, а ее эрзац, созданный искусственно. Выведем на орбиту в плоскость РТ диск (диаметром 90 км, расстояние от Земли 10 тыс. км). Пристроим перпендикулярно диску гантель (см. задачу «Гантель в космосе») длиной порядка 1000 км, тогда диск все время будет смотреть на Землю и будет неотличим от шара (впрочем, можно сделать и надувной шар). Зачерним половину диска (шара), а вторую сделаем люминесцирующей или прозрачной, тогда внутрь можно поместить источники света (питаемые от солнечной батареи, роль которой, возможно, удастся поручить зачерненной половине). Заказ исполнен. Правда, с помощью поддельной Луны, но подделки сейчас в большой моде у вышеупомянутого заказчика.

• Задача 72. Сириус увидеть нельзя

• Оглавление

Дата публикации:

26 июля 2004 года