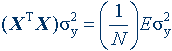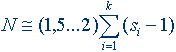Информационная коррекция погрешностей измерений

Информационная коррекция переменных систематических погрешностей средств измерений и измерительных информационных систем

Станислав РАДЧЕНКО
Павел БАБИЧ

Рецензент: Туз Ю.М.
директор НИИ АЭИ, д.т.н., проф., лауреат Государственной премии Украины в области науки и техники

УДК681.2.088

Вступление

Требования к точности, правильности и сходимости средств измерений постоянно возрастают. Повышение требований обычно проводилось путем перехода от используемого к новому физическому принципу измерения, который и обеспечивал более высокие качества измерений. Одновременно совершенствовались методика и техника проведения измерений, ужесточались требования к комплексу нормальных (стандартных) условий, сопровождающих процесс измерений.

Любые измерительные прибор, система, канал «реагируют» не только на измеряемую величину, но и на внешнюю среду, т.к. неизбежно связаны с нею.

Хорошей иллюстрацией этого теоретического тезиса может быть влияние приливных волн, вызванных Луной в земной коре, на изменение энергии заряженных частиц, полученных на большом кольцевом ускорителе в Центре европейских ядерных исследований. Приливная волна деформирует 27-километровое (2,7·10⁷ мм) кольцо ускорителя и изменяет длину пробега частиц по кольцу приблизительно на 1 мм (!). Это приводит к изменению энергии ускоренной частицы почти на десять миллионов электронвольт. Указанные изменения очень малы, но превышают возможную погрешность измерений примерно в десять раз и уже привели к серьезной ошибке в измерении массы бозона.

Постановка проблемы

Метрологическое обеспечение радиоэлектронных измерений может быть охарактеризовано следующей типичной проблематикой [1]. Использование теоретических методов анализа влияния факторов внешней среды на погрешности средств измерений затруднительно. Характер влияния сложен, нестабилен, трудно интерпретируем с позиций логически-профессионального анализа специалистом; изменчив при переходе от экземпляра к экземпляру одного и того же типа средств измерений [1, с. 111].

Отмечается методологическая сложность получения зависимостей неизвестного вида от нескольких переменных [1, с. 114] и то, что «...возможности исследования зависимостей погрешности от факторов внешней среды весьма ограничены и мало достоверны, особенно в отношении совместных влияний факторов и динамических изменений их значений» [1, с. 146].

В результате приведенных причин и значительного разнообразия их проявления делается вывод, что для группы средств измерений одного типа наиболее адекватным описанием погрешностей средств измерений от влияющих факторов внешней среды следует признать зону неопределенности, границы которой определяются крайними зависимостями экземпляров [1, с. 112].

Указанные трудности в решении проблемы уменьшения погрешностей средств измерений есть следствие системных свойств этих средств: эмергентности, целостности, неопределенности, сложности, стохастичности и др. [2, c. 57, рис. 2.1]. Попытки теоретического описания на уровне номографических наук в рассматриваемых ситуациях часто не эффективны. Необходим экспериментально-статистический подход, т. к. он позволяет провести идиографическое описание закономерности конкретных явлений в детальных условиях времени и места [2, с. 33...34].

Как в радиоэлектронных измерениях [1, с. 138], так и в обеспечении точности оценивания результатов количественного химического анализа [3, с. 1894...1897] отмечается важная особенность погрешностей: систематические погрешности результата для большинства средств измерений существенны в том смысле, что они превышают случайную, и погрешность данного экземпляра средства измерения в каждой точке факторного пространства определяется, в основном, постоянной величиной.

Для дальнейшего повышения качества проводимых измерений необходимо использовать не только физические – конструкторские, технологические, эксплуатационные – возможности, но и информационные. Они заключаются в реализации системного подхода в получении информации о всех видах погрешностей: инструментальных, методических, дополнительных, систематических, прогрессирующих (дрейфовых), модельных и возможно др. Имея такую информацию в виде многофакторной математической модели и зная значения факторов (условий), сопровождающих процесс измерения, можно получить информацию о приведенных погрешностях и, следовательно, более точно знать измеряемую величину.

Требования к методологии математического моделирования систематических погрешностей средств измерений

Необходимо разработать методику многофакторного математического моделирования закономерно изменяющихся систематических погрешностей с учетом следующих требований.

1. Системный подход к описанию систематических погрешностей с учетом множества факторов и, если необходимо, множества критериев качества средства измерения.
2. Прикладной уровень получения математических моделей, когда их структура исследователю не известна.
3. Эффективность (в статистическом смысле) получения полезной информации из исходных данных и отражение ее в математических моделях.
4. Возможность доступной и удобной содержательной интерпретации полученных моделей в предметной области.
5. Эффективность использования математических моделей в предметной области по сравнению с затратами ресурсов на их получение.

Основные этапы получения математических моделей

Рассмотрим основные этапы получения многофакторных математических моделей, соответствующих вышеприведенным требованиям.

Выбор плана многофакторного эксперимента, обеспечивающего необходимые свойства получаемых математических моделей

В рассматриваемом (метрологическом) классе проводимых экспериментальных исследований возможно использование полного и дробного факторного эксперимента. Под определяемой математической моделью будем понимать линейную относительно параметров и нелинейную в общем случае относительно факторов модель произвольно высокой, но конечной сложности. В расширенную матрицу эффектов полного факторного эксперимента будет входить столбец фиктивного фактора X₀ = 1, столбцы всех главных эффектов и всех возможных взаимодействий главных эффектов. Если эффекты факторов и взаимодействий факторов выразить в виде системы ортогональных нормированных контрастов, то матрица дисперсий-ковариаций примет вид:

где X – матрица эффектов полного факторного эксперимента;
σ_y² – дисперсия воспроизводимости результатов опытов;
N – число опытов в плане эксперимента;
Е – единичная матрица.

Математическая модель, полученная по схеме полного факторного эксперимента, соответствует многим замечательным свойствам: коэффициенты модели ортогональны друг другу и в статистическом смысле независимы; максимально устойчивы (cond = 1); каждый коэффициент несет семантическую информацию о влиянии соответствующего эффекта на моделируемый критерий качества; план эксперимента соответствует критериям D-, A-, E-, G-оптимальности, а также критерию пропорциональности частот уровней факторов; математическая модель адекватна в точках аппроксимации поверхности отклика [2, с. 102...103]. Будем считать такую модель истинной и «наилучшей».

В тех случаях, когда использование полного факторного эксперимента невозможно по причине большого числа опытов, следует рекомендовать применять многофакторные регулярные (желательно равномерные) планы экспериментов. При правильном выборе числа необходимых опытов их свойства максимально близки к приведенным свойствам полного факторного эксперимента [2, с. 115...118; 127...131].

Получение структуры многофакторной математической модели

Структуру получаемой многофакторной математической модели, в общем случае не известной исследователю, необходимо определять, исходя из возможного множества эффектов, соответствующих множеству эффектов схемы полного факторного эксперимента. Она задается выражением [2, с. 80]:

где X₁,..., X_k – факторы искомой математической модели;

s₁,..., s_k – число уровней факторов X₁,..., X_k;

k – общее число факторов;

N_п – число опытов полного факторного эксперимента, равное числу структурных элементов его схемы.

Поиск необходимых эффектов – главных и взаимодействий – в виде ортогональных контрастов для искомой модели осуществляется как многократная статистическая проверка гипотез о статистической значимости эффектов. В модель вводят статистически значимые эффекты.

Выбор числа необходимых опытов для дробного факторного эксперимента

Обычно исследователю известна (приближенно) информация о предполагаемой сложности влияния факторов на моделируемый критерий качества. Для каждого фактора выбирается число уровней его варьирования, которое должно быть на 1 больше максимальной степени полинома, необходимой для адекватного описания этим фактором поверхности отклика. Необходимое число экспериментов будет [2, с. 111]:

где s_i – число уровней фактора X_i ; 1 ≤ i ≤ k.

Коэффициент 1,5 выбирается для случая, когда число необходимых экспериментов значительно (порядка 50...64 и более). При меньшем необходимом числе экспериментов следует выбирать коэффициент 2.

Выбор структуры многофакторной математической модели

Для выбора структуры получаемой математической модели необходимо использовать разработанный алгоритм [2, с. 111...113]. В алгоритме реализована последовательная схема выделения необходимой структуры по результатам спланированного многофакторного эксперимента.

Обработка результатов экспериментов

Для комплексной обработки результатов экспериментов и получения необходимой информации для интерпретации результатов в предметной области разработано программное средство «Планирование, регрессия и анализ моделей» (ПС ПРИАМ) [2, c. 174...176; 4]. Разработчик – лаборатория экспериментально-статистических методов кафедры технологии машиностроения Национального технического университета Украины «Киевский политехнический институт». Оценка качества получаемых математических моделей включает следующие критерии:

• получение информативного подмножества главных эффектов и взаимодействий факторов для принятия в качестве структуры искомой многофакторной математической модели;
• обеспечение максимально высокой теоретической эффективности (вплоть до 100%) извлечения полезной информации из исходных данных;
• проверка на статистическую значимость потенциальной математической модели;
• проверки различных предпосылок множественного регрессионного анализа;
• проверка на адекватность полученной модели;
• проверка на информативность, т.е. присутствие в математической модели полезной информации и ее статистической значимости;
• проверка на устойчивость коэффициентов математической модели;
• проверка фактической эффективности извлечения полезной информации из исходных данных;
• оценка семантичности (информационной) по полученным коэффициентам математической модели;
• проверка свойств остатков;
• общая оценка свойств полученной математической модели и возможности ее использования для достижения поставленной цели.

Интерпретация полученных результатов

Осуществляется специалистом (или специалистами), хорошо понимающими как формальные результаты в полученных моделях, так и те прикладные цели, для достижения которых должны быть использованы модели.

Математический метод получения полезной информации о систематических погрешностях, сопровождающих процесс измерения физической величины, и средство измерения создают надсистему со взаимодействием (иначе эмергентностью) между собой. Эффект взаимодействия – более высокая точность измеряемой величины – принципиально нельзя получить только за счет отдельных подсистем. Это следует из структуры математической модели Ŷ (ŷ₁,..., ŷ_p) = f_j (СИ, ММ) для эксперимента 2²//4 (отсутствие подсистемы задается «–1», а присутствие «1») указанных подсистем:

где Ŷ (ŷ₁,..., ŷ_p) – вектор эффективности функционирования средства измерения, 1 ≤ j ≤ p;

1 – символ среднего значения результата (условное начало отсчета);

СИ – результат измерения, полученный только от средства измерения;

ММ – информация, полученная по многофакторной математической модели о систематических погрешностях используемого средства измерения при знании внутренних и внешних относительно его условий проведения замеров;

СИ · ММ – эффект взаимодействия (эмергентность) средства измерения и математической модели при условии их совместного использования.

Повышение точности измерения достигается за счет получения большего объема информации об условиях измерения и свойствах средства измерения во взаимодействии с внутренней и внешней относительно его средой.

Сочетание физических и информационных принципов на практике означает интеллектуализацию известных систем, в частности, создание интеллектуальных средств измерений. Объединение физических и информационных принципов в единую интегральную систему позволяет принципиально по-новому решать старые проблемы.

Пример повышения точности измерения цифровых весов

Рассмотрим возможности предложенного подхода на примере повышения точности цифровых весов с диапазоном взвешивания 0...100 кгс. Датчик весов емкостного типа с автономным питанием от переносного источника напряжения. Весы предназначены для эксплуатации в диапазоне температуры окружающей среды (воздуха) 0...60°С. Напряжение от автономного источника напряжения в процессе эксплуатации весов может изменяться в диапазоне 12,3...11,7 В при расчетном (номинальном) значении 12 В.

Предварительное исследование цифровых весов показало, что изменения температуры окружающей среды и питаемого напряжения в вышеприведенных диапазонах сравнительно мало влияют на показания емкостного датчика и, следовательно, на результаты взвешивания. Однако стабилизировать эти внешние и внутренние условия с необходимой точностью и поддерживать их в процессе функционирования весов не представлялось возможным ввиду того, что весы должны эксплуатироваться не в стационарных (лабораторных) условиях, а на борту перемещающегося объекта.

Исследование точности весов без учета влияния изменений температуры и питаемого напряжения показали, что средняя абсолютная погрешность аппроксимации составляет 0,16%, а среднеквадратичная погрешность остатка (в единицах измерения выходной величины взвешивания) равна 53,92.

Для получения многофакторной математической модели были приняты следующие обозначения факторов и значения их уровней.

X₁ – гистерезис. Уровни: 0 (нагрузка); 1 (разгрузка). Фактор качественный.

X₂ – температура окружающей среды. Уровни: 0; 22; 60°C.

X₃ – напряжение питания. Уровни:11,7; 12,0; 12,3 В.

X₄ – измеряемый вес. Уровни: 0; 20; 40; 60; 80; 100 кгс.

Учитывая принятые уровни варьирования факторов и сравнительно не трудоемкий объем испытаний было решено провести полный факторный эксперимент, т.е. 2 · 3² · 6//108. Исходные данные испытаний были предоставлены проф. П.В. Новицким. Каждый опыт был повторен только один раз, что нельзя признать хорошим решением. Желательно повторение каждого опыта два раза. Предварительный анализ исходных данных показал, что они со значительной вероятностью содержат грубые ошибки. Эти опыты были повторены и их результаты были исправлены.

Натуральные значения уровней варьирования факторов были преобразованы в ортогональные контрасты, иначе в систему ортогональных полиномов Чебышева.

С использованием системы ортогональных контрастов структура полного факторного эксперимента будет иметь следующий вид:

(1 + x₁) (1 + x₂ + z₂) (1 + x₃ + z₃) (1 + x₄ + z₄ + u₄ + v₄ + ω₄) → N₁₀₈

где x₁,..., x₄; z₂,..., z₄; u₄, v₄, ω₄ – соответственно линейные, квадратичные, кубический, четвертой и пятой степени контрасты факторов X₁,..., X₄;
N₁₀₈ – число структурных элементов для схемы полного факторного эксперимента.

Все эффекты (главные и взаимодействия) были нормированы

где x_iu^(p) – значение p-го ортогонального контраста i-го фактора для u-й строки матрицы планирования, 1 ≤ u ≤ 108, 1 ≤ p ≤ s_i – 1; 1 ≤ i ≤ 4.

Предварительный расчет математической модели показал, что в качестве оценки дисперсии воспроизводимости может быть выбрана (приближенно) величина 20,1.

Число степеней свободы (условно) принято V₂ = 108.

Дисперсия была использована для определения стандартной ошибки коэффициентов уравнения регрессии.

Вычисление математической модели и всех ее критериев качества было проведено с использованием ПС ПРИАМ. Полученная математическая модель имеет вид

где:

x₁ = 2 (X₁ – 0,5);

x₂ = 0,0306122 (X₂ – 27,3333);

z₂ = 1,96006 (x²₂ – 0,237337x₂ – 0,575594);

x₃ = 3.33333 (X₃ – 12);

z₃ = 1,5 (x²₃ – 0,666667);

x₄ = 0,02 (X₄ – 50);

z₄ = 1,875 (x²₄ – 0,466667);

u₄ = 3,72024 (x³₄ – 0,808x₄);

v₄ = 7,59549 (x⁴₄ – 1,08571x²₄ + 0,1296).

Таблица 1

Критерии качества полученной математической модели

Таблица 2

Статистические характеристики коэффициентов регрессии

b₀ = 28968,9
Уровень значимости для t-критерия – 0,05
Для степеней свободы V₁ = 108. Табличное значение t-критерия – 1,9821

В табл. 1 приведена распечатка критериев качества полученной многофакторной математической модели. Модель адекватна. Доля рассеивания, объясняемая моделью, весьма высока, т. к. модель высокоточная, изменчивость функции отклика велика, а ее случайная изменчивость сравнительно мала. Коэффициент множественной корреляции R весьма близок к 1 и устойчив, т. к. будучи скорректированным с учетом степеней свободы, практически не меняется. Статистическая значимость R весьма велика, т.е. модель очень информативна. Высокая информативность модели подтверждается также значением критерия Бокса и Веца. Коэффициенты модели максимально устойчивы: число обусловленности cond = 1. Полученная модель семантична в информационном смысле, т. к. все ее коэффициенты ортонормированны: они статистически независимы и могут сравниваться по абсолютной величине друг с другом. Знак коэффициента показывает характер влияния, а его абсолютная величина – силу влияния. Полученная модель наиболее удобна для интерпретации в предметной области.

Учитывая семантичные свойства полученной математической модели и доли участия каждого из эффектов модели в общей доле рассеивания, объясняемой моделью, можно провести содержательный информационный анализ формирования результата измерения исследуемых цифровых весов.

Превалирующая доля участия в результатах моделирования, равная 0,999557, создается линейным главным эффектом x₄ (с коэффициентом b₁ = –3715,13), т.е. измеряемым весом (табл. 2). Нелинейность z₄ (с коэффициентом b₅ = –19,07) сравнительно мала (3,16·10^–5) и ее учет в модели повышает точность измерения. Линейный эффект x₄ сравнительно слабо (3,19·10^–6) взаимодействует с квадратичным эффектом z₂ температуры окружающей среды: взаимодействие z₂x₄ (b₈ = –9,27). Следовательно, математическая модель только от фактора измеряемый вес X₄ должна включать и эффект влияния температуры окружающей среды

ŷ₁ = 28968,90 – 3715,13x₄ – 19,07z₄ – 9,27z₂x₄ ,

фактор которого X₂ является неуправляемым.

Напряжение питания изменяет результаты взвешивания в виде линейного эффекта x₃ (b₂ = 45,21) и квадратичного эффекта z₃ (b₆ = –19,66). Их суммарная доля участия составляет 2,41·10^–4.

Температура окружающей среды влияет в виде квадратичного z₂ (b₃ = –37,52) и линейного x₂ (b₄ = 23,17) эффектов с суммарной долей участия 1,60·10^–4.

Температура окружающей среды и напряжение питания образуют парное взаимодействие x₂z₃ (b₇ = –9,01) c долей участия 3,63·10^–6.

Доказательность статистической значимости двух последних эффектов x₁x₂ и z₂x₃ не может быть обоснована, т. к. они существенно меньше эффектов x₂z₃ и z₂x₄, а обоснованное значение дисперсии воспроизводимости по результатам повторных опытов в представленных исходных данных, к сожалению, отсутствовало.

В табл. 2 приведены статистические характеристики коэффициентов регрессии. Отметим, что значения коэффициентов регрессии разделены на нормировочные коэффициенты ортогональных контрастов, которые не включены в приведенные формулы ортогональных контрастов. Этим и объясняется то, что при делении значений коэффициентов регрессии на их стандартную ошибку полученные значения t-критерия отличаются от приведенных правильно вычисленных значений этого критерия в табл. 2.

Рис. 1. Гистограмма остатков

На рис. 1 показана гистограмма остатков . Она сравнительно близка к нормальному закону распределения. В табл. 3 представлены численные значения остатков и их проценты отклонений. Временной график остатков (рис. 2) указывает на случайный характер изменения остатков от времени (последовательности) проведения опытов. Дальнейшее повышение точности модели не возможно. Анализ зависимости остатков от ŷ (расчетного значения) показывает, что наибольшие разбросы остатков наблюдаются для X₄ = 0 кгс (y = 32581...32730) и X₄ = 100 кгс (y = 25124...25309). Наименьший разброс при X₄ = 40 кгс. Однако статистическая значимость такого заключения требует знания обоснованного значения дисперсии воспроизводимости.

Рис. 2. Временной график остатков

Учет в математической модели разнообразных систематических погрешностей, нелинейностей, взаимодействий неуправляемых факторов позволил повысить точность средства измерения по критерию средней абсолютной погрешности аппроксимации до 0,012% – в 13,3 раза, а по критерию среднеквадратичной погрешности аппроксимации до 4,80 (табл. 1) – в 11,2 раза.

План эксперимента 2²//4 для средней абсолютной погрешности аппроксимации в % и полученные результаты при использованиии только средства измерения и средства измерения с математической моделью систематической погрешностей представлен в табл. 4.

Математическая модель для средней абсолютной погрешности аппроксимации, полученная по эксперименту 2²//4, со структурой модели (1) и результатам функционирования средства измерения без математической модели и с ее использованием, имеет вид

ŷ = 0,043 + 0,043x₁...0,037x₂...0,037x₁x₂

где x₁ – ортогональный контраст фактора X₁ (СИ) – средство измерения;

x₂ – ортогональный контраст фактора X₂ (ММ) – математическая модель систематических погрешностей используемого средства измерения;

x₁x₂ – взаимодействие факторов X₁ (СИ) и X₂ (ММ).

Таблица 4

План эксперимента 2²//4

Анализ коэффициентов модели показывает, что фактор X₂ (ММ) уменьшает систематическую погрешность не только в виде главного эффекта x₂ (коэффициент b₂ = –0,037), но и за счет взаимодействия (эмергентности) факторов X₁ (СИ) · X₂ (ММ) (коэффициент b₁₂ = –0,037).

Аналогичную модель можно получить и для критерия среднеквадратичной погрешности аппроксимации.

Для фактической реализации полученной модели (2) необходимо измерить и использовать информацию о температуре окружающей среды и напряжении питания с помощью датчиков и провести расчет результата с применением микропроцессора.

Результаты математического моделирования шестикомпонентных тензометрических измерительных систем

В [2, с. 192...197; 5] рассмотрено математическое моделирование шестикомпонентных тензометрических измерительных систем. Предложенный метод был внедрен на Киевском механическом заводе (ныне Авиационный научно-технический комплекс им. О.К. Антонова). Впервые в практике проведения аналогичных измерений этот метод в значительной степени позволил исключить последствия физических несовершенств измерительных систем, проявляющихся в виде взаимодействия между каналами, влияния других каналов на рассматриваемый канал, нелинейностей и изучить структурные взаимосвязи различных каналов.

Использование метода математического моделирования в реальных условиях предприятия показало, что время проведения опытов сокращается в 10...15 раз; существенно (до 60 раз) повышается эффективность обработки измерительной информации; в 2...3 раза сокращается количество исполнителей, занятых в измерительных экспериментах.

Итоговый вывод о целесообразности использования изложенного подхода зависит от экономической эффективности следующих сравниваемых вариантов.

Высокоточного средства измерения и, следовательно, более дорогого, используемого в нормированных (стандартных) условиях, которые необходимо создать и поддерживать.

Средства измерения менее высокой точности, используемого в не нормированных (не стандартных) условиях с применением полученной математической модели.

Основные выводы

1) Успешно реализованный системный подход в математическом моделировании средства измерения позволил учесть влияние факторов внешней – температура окружающей среды – и внутренней среды – напряжение питания. Эффективность извлечения полезной информации из исходных данных составила 100%.

2) В полученной многофакторной математической модели, структура которой априори исследователю не была известна, в удобной для интерпретации в предметной области форме раскрыты нелинейность средства измерения и системное влияние факторов (эмергентность) внешней и внутренней среды. В реальных условиях эксплуатации стабилизация этих факторов с необходимой точностью не представляется возможной.

3) Учет математической модели систематических погрешностей позволил повысить точность измерений по критерию средней абсолютной погрешности в 13,3 раза и по критерию среднеквадратичной погрешности в 11,2 раза.

Наши предложения

Лаборатория экспериментально-статистических методов и исследований готова предоставить алгоритмическое, программное обеспечение для получения многофакторных математических моделей, их анализа и интерпретации и передать накопленный опыт для использования при решении конкретных производственных и научных задач.

Мы готовы решить Ваши проблемы в указанных и многих других областях путем использования созданных за многие годы алгоритмов, программного обеспечения, ноу-хау; учебы и передачи опыта Вашим специалистам.

Контактная информация: http://n-t.ru/sp/lesmi/

Литература:

1. Рыбаков И.Н. Основы точности и метрологического обеспечения радиоэлектронных измерений. – М.: Изд-во стандартов, 1990. – 180 с.
2. Радченко С.Г. Математическое моделирование технологических процессов в машиностроении.– К.: ЗАО «Укрспецмонтажпроект», 1998. – 274 с.
3. Алимов Ю.И., Шаевич А.Б. Методологические особенности оценивания результатов количественного химического анализа // Журнал аналитической химии. – 1988. – Вып. 10. – Т. XLIII. – С. 1893...1916.
4. Планирование, регрессия и анализ моделей PRIAM (ПРИАМ). SCMC–90; 325, 660, 668 // Каталог. Программные продукты Украины. Catalog. Software of Ukraine. – К.: СП «Текнор». – 1993. – C. 24...27.
5. Зинченко В.П., Радченко С.Г. Метод моделирования многокомпонентных тензометрических измерительных систем. – К.: 1993. – 17 с. (Препр. / АН Украины. Ин-т кибернетики им. В.М.Глушкова; 93...31).

Дата публикации:

18 мая 2000 года