| N-T.ru / Совместные проекты / ЛЭСМИ |
Планирование эксперимента в нестандартных областях факторного пространстваУДК 519.242:519.233.5 Постановка проблемыМногофакторные статистические модели получили значительное распространение в научных и прикладных исследованиях. Они используются при создании и совершенствовании различных сложных систем. Статистические модели особенно необходимы в тех случаях, когда возможности конструирования, производства и эксплуатации, основанные на традиционных физических принципах, исчерпаны или приводят к нецелесообразно большим затратам. При получении статистических регрессионных моделей необходимо использовать методологию теории планирования эксперимента [1, 2]. Известные традиционные методы планирования многофакторного эксперимента предполагают формы факторных пространств в виде многомерных прямоугольного параллелепипеда (куба), сферы и симплекса. В нестандартных областях факторного пространства поиск наилучших условий получения моделей в общем виде по публикациям не известен, кроме метода регуляризации. Единичные случаи таких задач решались численными методами. Анализ достижений и публикаций по теме исследованияПричины возникновения нестандартных областей факторного пространства следующие: 1) параметры (факторы) однородного ряда технических и технологических объектов связаны зависимостью близкой к линейной [3, с. 338], 2) обработка результатов эксперимента при условии, что уровни факторов не могут быть достаточно точно выдержаны по матрице плана эксперимента, 3) Обработка результатов пассивного (специально не организованного) эксперимента. В нестандартных областях факторного пространства наблюдается корреляция факторов и, следовательно, их главных эффектов и взаимодействий при построении регрессионных моделей. Мультиколлинеарность эффектов (взаимная сопряженность их) затрудняет или делает невозможным устойчивое определение структуры и коэффициентов уравнения регрессии, содержательную интерпретацию причинных и структурных связей между эффектами и моделируемым откликом. При значительной мультиколлинеарности эффектов задача является некорректно поставленной и целесообразное использование уравнения регрессии теряет смысл. Редактор русского перевода сборника статей [4] д.ф.-м.н. Н.Г. Волков считает, что «необходимы устойчивые методы и алгоритмы, обладающие ясными математическими свойствами в смысле их оптимальности» [4, с. 6]. Особенностью широко используемого при получении статистических моделей метода наименьших квадратов является его неустойчивость, «если не делать каких-то дополнительных предположений, которые трудно проверяемы» [5, с. 94]. Поэтому при решении прикладной задачи необходимо, по мнению исследователя, не только сформулировать систему необходимых предпосылок, но и методики их проверок [6]; устойчивость предпосылок и метода получения моделей к сравнительно малым нарушениям принятых условий; систему действий исследователя, если принятые предпосылки не выполняются фактически [7, с. 55...65]. Ведущий научный сотрудник механико-математического факультета МГУ им. М.В. Ломоносова А.М. Шурыгин, обсуждая проблему устойчивости оценивания параметров распределения и статистических моделей, приходит к следующему выводу. «В классической статистике отсутствует понятие устойчивости решения, и этим она невыгодно отличается от других ветвей прикладной математики. Предполагается, что если решение оптимально в рассматриваемой модели, то в похожей модели оно будет близко к оптимальному. Но такое предположение не обосновано. На «неуниверсальность» оценок максимума правдоподобия указывал А.Н. Колмогоров» [8, c. 161]. Некоторые специалисты констатируют сложность и трудность решения проблемы мультиколлинеарности: «Однозначного ответа на этот вопрос нет» [9, c. 94]. Цель статьиОбоснование методов устойчивого оценивания структуры и коэффициентов многофакторных статистических моделей для произвольных (нестандартных) форм факторного пространства с наилучшими возможными критериями качества полученных моделей. Основная частьФакторное пространство, соответствующее многомерному прямоугольному параллелепипеду, принимается за прообраз факторного пространства Rпр. Используя методы планирования эксперимента, в прообразе всегда можно получить статистические модели с наилучшими характеристиками. Произвольная область факторного пространства, не соответствующая стандартной форме, принимается за образ факторного пространства Rо. Получить в нем статистические модели с наилучшими характеристиками традиционными методами не представляется возможным. Необходимо найти метод перехода от заданного плохо обусловленного факторного пространства Rо образа к хорошо обусловленному факторному пространству Rпр прообраза, в котором и необходимо решать поставленную задачу. Впервые предложено использовать топологическое отображение прообраза факторного пространства в образ факторного пространства [7, c. 190...197]. Две системы Rпр и Rо при взаимно однозначном и взаимно непрерывном отображении будут изоморфными, т. е. равными по виду, форме. Понятие изоморфизма включает в себя как частный случай понятие гомеоморфизма. Гомеоморфные пространства топологически эквивалентны. При рассмотрении топологического отображения метрические свойства множеств Xпр (прообраз) и Xо (образ) не используются. Следовательно, отображаемые множества Xпр, Xо могут характеризоваться различными метрическими свойствами. Сформулированы в общем виде пять методов ортогонального представления коррелированных факторов. 1) Ортогональность представления коррелированных факторов путем отображения точек прообраза – значений уровней факторов Xiuпр в соответствующие им точки образа – значения уровней факторов Xiuо (1 ≤ i ≤ k, 1 ≤ u ≤ N) [7, c. 195].
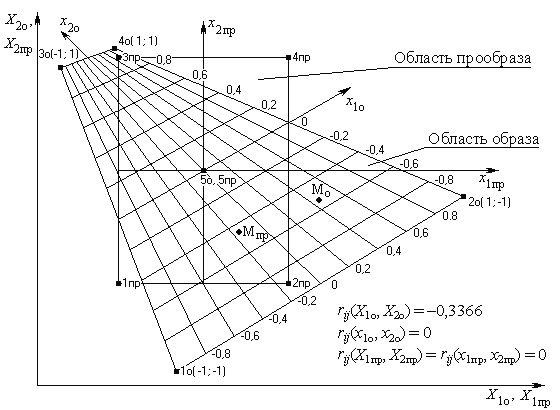
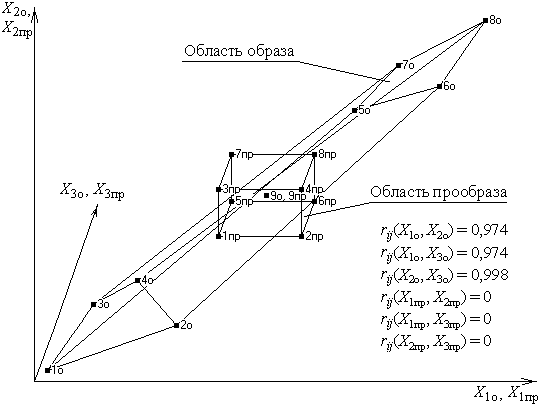
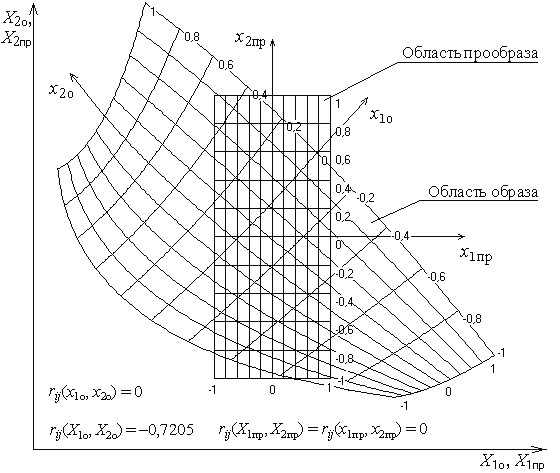
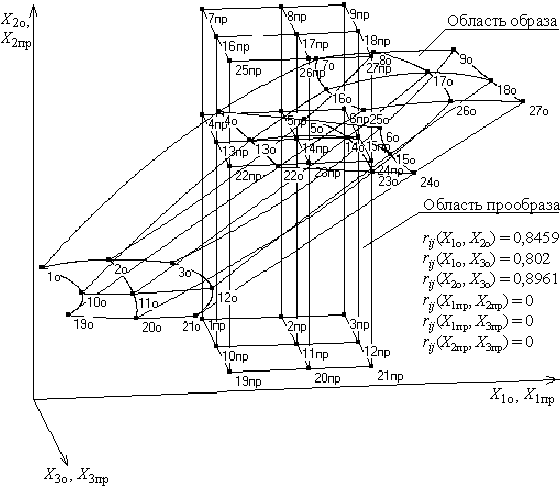
Функции fiотоб и обратные функции fiотоб–1 должны быть непрерывны. Функции отображения fiотоб впервые предлагается для случая линейного ограничения формы образа задавать в виде структуры полного факторного эксперимента 2k. (1 + x1)(1 + x2)...(1 + xk) → NП. Для случая криволинейного ограничения формы образа впервые предлагается использовать ограничительные линии второго порядка и криволинейные поверхности, полученные на основе структуры многофакторного эксперимента 3k или 3k–p. (1 + x1 + z1)(1 + x2 + z2)...(1 + xk + zk) → NП(NД), где 1 – значение фиктивной независимой переменной x0 ≡ 1; x1, x2, ..., xk – линейные ортогональные контрасты факторов X1, X2, ..., Xk; z1, z2, ..., zk – квадратичные ортогональные контрасты факторов X1, X2, ..., Xk; k – число факторов; NП(NД) – общее число структурных элементов, равное соответственно 2k, 3k или 3k–p; p – дробность реплики; p = 1; 2 для k = 4; 5. Предполагается, что k = 2, ..., 5. Коэффициенты функции отображения fiотоб определяют, используя метод наименьших квадратов. На рис. 1, 2 и рис. 3, 4 показаны области образа и прообраза соответственно при линейных и криволинейных ограничениях образа для k = 2; 3. Однозначность функции fiотоб–1 была подтверждена путем анализа якобиана: в области прообраза он не равен нулю. Коэффициенты парной корреляции факторов rij(Xiо, Xjо) в образе отличны от нуля, а в собственных кодированных координатах образа rij(xiо, xjо) и в прообразе rij(Xiпр, Xjпр) равны нулю.
Рис. 1. Системы натуральных и собственных кодированных координат областей образа и прообраза при линейном ограничении образа, k = 2
Рис. 2. Области образа и прообраза при линейном ограничении образа, k = 3 Отображение точек плана эксперимента Xiuпр прообраза в точки Xiuо образа с использованием функций отображения (1) фактически представляет получение плана эксперимента в образе при условии использования в прообразе и образе собственной кодированной системы координат (рис. 3). Хорошие свойства оценок коэффициентов статистических моделей в области прообраза и их единственность сохраняется при топологическом отображении и в области образа, что следует из доказанной проф. Т. Андерсоном леммы 3.2.3 и следствия из нее 3.2.1 [10, c. 69].
Рис. 3. Системы натуральных и собственных кодированных координат областей образа и прообраза при криволинейном ограничении образа, k = 2
Рис. 4. Области образа и прообраза при криволинейном ограничении образа, k = 3 В основу исследования и обоснования топологического отображения принята теория групп преобразований. Фигуры прообраза Фпр и образа Фо находятся в отношении эквивалентности, так как для них выполняются бинарные отношения эквивалентности: рефлексивность, симметричность, транзитивность. Гомеоморфность фигур Фпр и Фо была подтверждена проведенным вычислительным экспериментом [7, c. 295...298]. Другие методы и подходы устойчивого оценивания статистических моделей: 2) установление собственной кодированной системы координат в области прообраза и в области образа [7, c. 286...289], 3) планирование эксперимента с использованием фиктивных факторов [7, c. 328...341], 4) применение сложных функций [7, c. 341...344], 5) выбор оптимальных координат факторного пространства [7, c. 344...351]. Выводы и перспективы дальнейших исследований1. Впервые предложен, разработан и обоснован метод гомеоморфного отображения для построения оптимальных планов экспериментов и повышения устойчивости регрессионных моделей в условиях взаимной сопряженности факторов. 2. При использовании разработанного метода устойчивого оценивания в произвольной по форме факторном пространстве образа можно планировать эксперимент и получать наилучшие возможные критерии качества статистических моделей. В дальнейшем необходимо продолжить разработку анализа вкладов эффектов факторов Xiо по полученным статистическим моделям в области образа.
Литература:
Ранее опубликовано: Радченко С.Г. Планирование эксперимента в нестандартных областях факторного пространства // Вестник ХНТУ. – 2007. – №2(28). – С. 281...285: ил. 4. – Библиогр.: 10 назв. |
|
Дата публикации: 6 октября 2007 года |
|