Долгое прощание с лысенковщиной

В.П. ЛЕОНОВ

Часть 5

Камуфляжные мемы

Отметим, что камуфляжный характер описания статистических методов встречается не так уж редко, и, как правило, в диссертациях. Рассмотрим пример, показывающий рекомбинацию ранее встречавшихся нам мемов с другими мемами. На стр. 41 кандидатской диссертации №13 – Клинико-диагностические критерии нарушений сердечно-сосудистой системы у детей с тимомегалией.). Канд. дисс., 14.00.09 – педиатрия, 1996 г. дано следующее описание. «Статистический анализ проводился на основе банка данных, доступ к которому реализовывался через пакет программ STATGRAPHICS в которой (так в тексте – В.Л.) использовались вариационный, корреляционный, регрессивный и дискриминантный методы, помимо средних значений расчитывались (так в тексте – В.Л.) величины дисперсий первого и второго порядка, определялась погрешность и достоверность, оценка параметров проводилась по Т-критерию Стьюдента». С предыдущей работой эту диссертацию роднит не только близость научного направления и объекта исследования, но и наличие мема «на основе банка данных, доступ к которому реализовывался через пакет программ». Имеется здесь и часть других мемов, в частности упоминание «вариационного» и «регрессивного» анализа. Если под «регрессивным» анализом автор видимо подразумевала регрессионный анализ, то, что такое «вариационный анализ», можно только гадать. Упоминание о таинственном «вариационном анализе» можно встретить и в других публикациях, например, на стр. 42 диссертации №14 – Иммуно-патохимические особенности течения респираторных аллергозов у детей. Канд. дисс., 14.00.09 – педиатрия, 14.00.36 – аллергология и иммунология, 1997 г.

Следующее ядро мема – «дисперсии первого и второго порядка». Наиболее вероятной гипотезой появления этого мема является рекомбинация определения термина дисперсия и определений начальных и центральных моментов. Как известно, начальный момент первого порядка есть не что иное, как математическое ожидание, а центральный момент второго порядка и есть дисперсия [103, с.92...99]. Судя по приведенному выше описанию, автором «определялась погрешность и достоверность». Видимо полагая, что эти определяемые величины не требуют дополнительного комментария, автор не поясняет ни смысл этих величин, ни методику их определения. Не меньше вопросов вызывает и то, как «оценка параметров проводилась по Т-критерию Стьюдента». В частности, из этого отрывка совершенно непонятно, оценка каких именно параметров проводилась автором с помощью Т-критерия Стьюдента. Ответов на эти вопросы в тексте диссертации нет, как нет и описания того, с помощью каких статистических критериев проводились проверки многочисленных гипотез, после чего появлялись выражения p < 0,05. Нет там и результатов «регрессивного» и дискриминантного анализа.

Анализ многочисленных биомедицинских диссертаций обнаруживает два вида камуфляжных мемов. В первом случае автор декларирует в описании те или иные статистические методы или критерии, использованные им в исследовании. Однако далее в тексте не приводит никакой информации ассоциирующейся с результатами применения этих методов. В качестве типичного случая камуфляжного мема первого типа можно привести описание из кандидатской диссертации «Арефлюксные гастротома и еюностома (Экспериментально-клиническое исследование)», 14.00.27 – хирургия, 1996 г. На стр. 38 имеется следующее описание: «Фактические данные обработаны методами математической статистики для малых выборок на ЭВМ:

• метод сравнения средних:
• метод сравнения дисперсий:
• проверка гипотиз (так в тексте – В.Л.) по критерию «хи-квадрат».

Однако во всем дальнейшем тексте диссертации нет даже малейших намеков на результаты применения этих методов математической статистики. Нет ни привычных выражений M±m и p < 0,05, отсутствуют сами проверяемые «гипотизы» и обсуждение результатов их проверки, отсутствуют результаты обработки фактических данных методами математической статистики и в «Заключении» и в «Выводах».

Камуфляжный характер таких меметических описаний виден читателю не сразу. Иногда заметить это под силу только подготовленному специалисту, имеющему как определенный запас знаний по статистике, так и самостоятельный опыт статистического анализа биомедицинских данных. В качестве примера такого мема дадим следующее описание. «Нормальность распределения результатов во всех сформированных группах определяли путем подсчета асимметрии и эксцесса выборки. Для сравнения групповых средних и вариаций использовали параметрический t-критерий Стьюдента. Для оценки линейной стохастической связи между показателями флуоресцентных зондов и процентным содержанием морфологических форм эритроцитов в исследуемых группах использовали линейный корреляционный анализ.» – стр. 46 диссертации «Характеристика состояния мембраны эритроцитов периферической крови у детей в норме, с инсулинзависимым сахарным диабетом и острой пневмонией», 14.00.17 – нормальная физиология, 14.00.16 – пат. физиология, 1998 г. Казалось бы это вполне респектабельное описание, содержащее и упоминание о проверке на нормальность распределения, и о критерии Стьюдента, и о корреляционном анализе. Начнем с проверки нормальности распределения. Действительно, как один из самых простейших методов приближенной проверки нормальности распределения исследуемой непрерывной переменной в статистике используется оценка с помощью вычисления коэффициентов асимметрии и эксцесса [79, 103]. Однако автор не дает ни ссылки на литературный источник с описанием этого метода, не описывает детали того, каким образом производился подсчет этих показателей. Нет и описания того правила, по которому принималось решение о признании распределения нормальным, или же нормальность распределения отвергалась. Обращает на себя внимание полное отсутствие в диссертации любой информации о результатах как вычислений асимметрии и эксцесса, так и о результатах проверки нормальности распределения по этим показателям. Весьма маловероятно, чтобы все исследуемые характеристики состояния мембран эритроцитов во всех группах подчинялись нормальному распределению. Настораживает и отсутствие даже упоминания дальнейших действий в случае появления распределения, не подчиняющегося нормальному закону. В следующем предложении автор говорит о сравнении не только групповых средних, но и вариаций. И здесь автор тоже не идет дальше самого термина, не раскрывая ни его суть, ни технологию сравнения этих самых вариаций. Если предположить, что под вариациями автор понимает внутригрупповые дисперсии, то в этом случае для проверки их равенства используется не t-критерий Стьюдента, а другие критерии, например критерии Фишера, Кохрэна и Бартлетта. Опять же, далее в тексте автор ничего не говорит о результатах таких проверок, равны ли были групповые вариации, или же они были неравными, остается загадкой. Кстати, проведенная нами проверка нескольких сот выражений «M + m» с «p < 0,05» приведенных в диссертациях и статьях, где для проверки гипотезы о равенстве средних применяли t-критерий Стьюдента, показала, что примерно в 75% случаев дисперсии двух совокупностей оказываются неравными. Это означает, что t-критерий Стьюдента применять нельзя. Наконец, неизвестно и то, какой же именно коэффициент корреляции использовал автор: Пирсона или Спирмена, парный или частный. Таким образом, результаты проведенного нами анализа этого описания позволяют высказать весьма вероятное предположение о том, что оно является мемом, синтезированным из нескольких отдельных элементов.

Противоположный тип камуфляжных мемов состоит из описания некоторых полученных в исследовании статистических результатов, при том, что эти использованные методы и критерии нигде в диссертации ранее не описаны. Типичная диссертация, в изобилии содержащая такие мемы, «Влияние закаливания на состояние адаптационно-защитных механизмов у часто болеющих детей дошкольного возраста», 14.00.09 – педиатрия, 1991 г. В данной работе приведено несколько сот выражений типа «M±m» и «p < 0,05», или «p > 0,05». В самом тексте работы и в «Заключении» многократно встречаются выражения следующего вида: «Исследования исходного уровня клеточного иммунитета зафиксировало статистически достоверное (Р < 0,01) уменьшение абсолютного и относительного содержания Т-лимфоцитов у ЧБД» (стр. 115); «Динамическое наблюдение позволило установить, что статистически достоверное изменение в иммунном статусе под влиянием закаливающих процедур произошли в срок от полутора до трех месяцев» (стр. 117); «Таким образом, статистически достоверные динамические изменения в иммунном статусе у ЧБД, занимающихся закаливанием, выявлены в срок от полутора до трех месяцев от начала закаливания» (стр. 118). Однако в главе, посвященной использованным диссертантом методам и методикам, ничего не говорится о тех статистических методах и критериях, с помощью которых были получены декларируемые автором достоверные уменьшения и изменения. В таких случаях диссертационный совет, эксперты ВАК РФ и специалисты, желающие познакомиться с результатами диссертанта, могут оценивать достоверность этих результатов не с помощью квалифицированного описания этапа анализа данных, а только основываясь на собственном впечатлении о том, насколько выводы диссертанта совпадают или противоречат основным концепциям и положениям данного научного направления на текущий момент времени.

Точно также отсутствуют всяческие описания использованных статистических методов и в докторской диссертации «Влияние возраста на динамику и соотношение различных механизмов энергетического обеспечения гомеостаза в процессе мышечной деятельности», 14.00.17 – нормальная физиология, 1991 г. Между тем, работа полностью базируется на экспериментальных результатах. В тексте диссертации есть много выражений, оперирующих понятиями «достоверность» и «недостоверность». Приведем некоторые из них. «Так если у старых животных оно достоверно увеличивалось с исходных 5,05±0,55 до 7,29±0,29 г% (P < 0,001) уже в первую минуту бега, то у взрослых подъем с фоновых 6,36±0,14 до 6,90±0,19 г% становится достоверным лишь на 10 минуте бега» – стр. 88. «Результаты наших исследований (Рис. 10) показали, что содержание мочевины в артериальной крови при беге на тредбане повышается как у взрослых, так и у старых собак. Но у взрослых при более высоком исходном уровне ее прирост к фоновым значениям во время бега недостоверен. Достоверность появляется лишь в конце изучаемого восстановительного периода, спустя 50...80 минут после работы. У старых собак достоверный рост содержания мочевины в артериальной крови наступает уже в первую минуту бега, сохраняется до его окончания и в течение всего исследуемого восстановительного периода. Достоверность этой закономерности подтверждается данными о динамике содержания в артериальной крови аммиака (Рис. 11)» – стр. 90. «Достоверность такого рода данных, очевидно очень низка...» – стр. 113. Вопрос о том, какими именно методами автор проверял достоверность своих утверждений, важен еще и потому, что в тексте есть много таких результатов, которые без подробного объяснения этих методов нельзя адекватно понять и оценить. Так, на 124 графиках приведенных в диссертации обозначены положительные и отрицательные отклонения от линии графика. Какой смысл имеют эти отклонения, нигде не расшифровывается. Являются ли эти отрезки доверительным интервалом, или же они изображают величину ошибки среднего в данной точке графика, нигде не уточняется. Между тем, это имеет принципиальное значение. Для подтверждения важности подробного описания этих деталей приводимых в работе результатов анализа рассмотрим еще одно предложение. «Если учесть многочисленные литературные данные последних лет, указывающие, что колебания максимального потребления кислорода лежат в пределах 36,0±5,1 – 66±5,0 мл/кг/мин или 3,35±4,27 л/мин, что физиологической нормой энергозатрат при профессиональном труде являются 3,33±0,5 ккал/мин, что бег со скоростью 9...12 км/час сопровождается энергозатратами 9...12 ккал/мин, то моделируемая в наших опытах негрузка в виде бега 11 и 12 км/час, притекающий с потреблением кислорода около 40 мл/кг/мин и частоте сердцебиений 160...180 в минуту, являются нагрузкой, приближающейся к тяжелой.» – стр. 49. Обратим наше внимание на выделенное нами выражение 3,35±4,27 л/мин. Какой смысл имеет это сочетание? Если это наиболее часто используемое выражение M±m, где М – среднее, а m – ошибка среднего, то в этом случае получается что ошибка среднего превосходит саму величину среднего. А в таком случае это прямое указание на то, что в выборке, по элементам которой и вычислены М и m, есть и немало и отрицательных значений исследуемой переменной. Но по своему смыслу эта переменная – потребление кислорода, не может принимать отрицательных значений. Итак, какой же смысл имеет выражение 3,35±4,27 л/мин ?

Для большинства проанализированных работ наблюдалось влияние принадлежности авторов исследований к той или иной научной школе на уровень описания использованных в работе статистических методов. Как правило, работы по близкой тематике имели и практически идентичный набор использованных методов. Для примера приведем описания из кандидатской и докторской диссертаций на близкие темы. «Все полученные данные обрабатывались на ЭВМ «Kontron» и «Casio FX-790 P» методом вариационной статистики с вычислением среднего арифметической «Х», средней ошибки средней арифметической «m» и среднего квадратичного отклонения «?». Сравнение средних значений показателей производилось с использованием критерия Стьюдента, вычисляемого по формуле: (M 12 – M 22)/(m 12 + m 22). Доверительную вероятность «Р» определяли, исходя из рассчитанного значения t. Различие двух сравниваемых рядов считали достоверным, если вероятность их тождества P Ј 0,05. В тех случаях, когда распределение вариант внутри сравниваемых выборок отличалось от нормального, величину Р определяли с помощью непараметрического критерия Уилкоксона-Манна-Уитни» – стр. 57 кандидатской диссертации «Роль гемопоэзининдуцирующего микроокружения в регуляции кроветворения при гемодепрессии, вызванной введением адриамицина», 14.00.16 – пат. физиология, 14.00.25 – фармакология, 1990 г. Обратим внимание читателей на отсутствие квадратного корня в знаменателе дроби, тогда как для t-критерия Стьюдента в этой формуле здесь должен быть знак квадратного корня. Как видно из этого описания, автор ограничился вычислением среднего М, средней ошибки среднего m и среднего квадратичного отклонения ?. Для проверки же гипотез о равенстве групповых генеральных средних использовались критерии Стьюдента и Уилкоксона-Манна-Уитни. Однако ни слова автор не упомянул о том, а какими же методами и критериями проверялась нормальность распределений внутри групп. Неясен и смысл фразы «Различие двух сравниваемых рядов считали достоверным, если вероятность их тождества P Ј 0,05», из которой следует, что в том случае, когда «вероятность их тождества» была больше 0,05, например 0,10, то различие двух сравниваемых рядов считалось недостоверным, но тогда это означает принятие противоположной гипотезы о равенстве сравниваемых рядов. В тексте самой работы 24 таблицы содержащих несколько сот выражений типа «M±m» и «р < 0,05» или «р > 0,05». Однако нигде нет указаний на то, каким критерием проверялась та или иная гипотеза, и каков был результат проверки нормальности распределения.

Обратимся теперь к докторской диссертации «Роль гемопоэзининдуцирующего микроокружения в регуляции кроветворения при действии на организм миелоингибирующих факторов», 14.00.16 – пат. физиология, 1994 г. На стр. 82 приведено следующее описания использованных статистических методов. «Полученные данные подвергали статистической обработке, используя методы вариационной статистики. При этом вычисляли среднюю арифметическую «Х» и среднюю ошибку среднего значения «m» в каждой группе. Проверку достоверности различий оценивали с помощью t-критерия Стьюдента (Лакин Г.Ф., 1973). Результаты исследования были обработаны на персональном компьютере IBM PC AT с использованием соответствующих программ. В таблицах приведены средние значения Х и средние ошибки величины (Х + m), на графиках – величины доверительных интервалов при Р = 0,05». Итак, в этой работе автор использует уже несколько методов вариационной статистики, отказавшись от проверки нормальности распределения и применения критерия Уилкоксона-Манна-Уитни и ограничившись одним критерием Стьюдента. Только почему то с его помощью оценивали уже не лостоверность различий (видимо групповых средних), а оценивали «Проверку». Интересно, как можно оценить «Проверку»? Сменился и тип компьютера, появилась ссылка на «соответствующие программы», неясно только какие. Но особо принципиальных различий в наборе методов как в одной, так и в другой диссертации не наблюдается. Фактически весь набор статистического инструментария сведен к вычислению простейших выборочных статистик и сравнению групповых средних. Также во второй работе, как и в первой, приведено несколько десятков (56) таблиц с выражениями «M ± m» и «р < 0,05». Отметим, что кроме схожести названий этих работ, их объединяет и то, что оба научных руководителя кандидатской диссертации являлись научными консультантами в докторской диссертации.

Смутно пишут о том, о чем смутно представляют

Об уровне использования статистических методов можно судить и по типичным грамматическим ошибкам, встречающимся в этом разделе. Так, популярный статистический пакет STATGRAPHICS часто упоминается с ошибочным написанием: STATGRAFICS, STATGRAFIKS, STATGRAPHIKS, Stat-graf, STATG, или STATGRAF (см. например, Зоологический журнал, 1998 г., том 77, №5, стр. 593).

В диссертации «Функциональное состояние эпифиза у женщин вне и во время беременности» (14.00.01 – акушерство и гинекология, 1994 г.) мы встретили даже такое утверждение: «Статистическая обработка полученных результатов производилась на компьютере 386DX по программе STATGRAF, основанной на методе Стьюдента». Между тем, статистический пакет STATGRAPHICS, разработанный американской корпорацией Manugistics (до 1 мая 1992 эта корпорация называлась Scientific Time Sharing Corp.) и к настояшему времени иемющий более 7 версий, включает в себя более 250 процедур анализа данных по 11 основным направлениям. В 1994 г. корпорации Manugistics и Statistical Graphics выпустили версию STATGRAPHICS 7 Plus for Windows, стоимостью 1695 долларов США и считающейся одной из наиболее удобных программ статистического анализа данных. Утверждать, что подобная программа основана на методе Стьюдента, это тоже самое, что сказать будто самолет основан на одном из кресел, стоящих внутри лайнера.

Искажаются наименования не только пакетов программ, но и названия того или иного вида анализа, языков программирования и названия книг, фамилии статистиков – авторов того или иного критерия. Известный табличный редактор Microsoft Excel на трех страницах одного и того же выпуска журнала «Кардиология» (вып. 8, 1997 г.), имеет три разных названия: на стр. 6 это «Excell», далее на стр. 8 это «Excel» а еще далее на стр. 11 уже другое название – «EXEL». В вып.12 за 1995 г. журнала «Кардиология» на стр. 19 дано следующее исчерпывающее описание использованных методов: «Статистическая обработка результатов проводилась на компьютере по программе «SC = 4». Только искушенный в области программного обеспечения специалист может предположить, что авторы, видимо, имели в виду программу электронных таблиц SuperCalc-4, нередко обозначаемую как SC 4.

На одной и той же странице можно встретить разные названия одного и того же вида анализа: «двухфакторный регрессионный анализ» и «двухфакторный регрессивный анализ» (Медицинская радиология и радиационная безопасность. 1996, том 41, вып. 5, стр. 5).

Ссылка на известную книгу по статистическому анализу в медицине «Статистический анализ: Подход с использованием ЭВМ» [50], дается в следующем написании: «Статистический анализ: Подход к использованию ЭВМ» (выделено нами – В.Л.).

На стр. 53 диссертации «Диагностическое и прогностическое значение увеличения щитовидной железы у детей и подростков», 14.00.09 – педиатрия, 1997 г. читаем: «Математический анализ материала методом процентилей выполнен вычислительной машиной СМ-4, программа для которой была составлена на языке Basik».

Вот как назван известный непараметрический критерий в диссертации «Состояние здоровья и функция некоторых желез внутренней секреции у детей из зоны радиоактивного следа» (14.00.09 – педиатрия, 1997 г.): «Статистическая обработка проводилась с использованием вычислительной техники методом вариационной статистики с вычислением средней величины и средней ошибки, достоверности различия между средними определялась по критерию Стьюдента (при малых выборках Вильконсона-Мана-Уитни» (стр. 29). На первый взгляд это мелочь, что автор вместо Вилкоксона написал Вильконсона, вместо Манна написал Мана и т.д. Однако этот симптом говорит о том, что владение этим критерием у кокретного автора не стало столь обыденным делом, что хорошо запомнились не только особенности самого метода, но и фамилии авторов этого метода и критерия. Об этом говорит и построение фразы, согласно которой этот критерий применяется для малых выборок, а для больших выборок можно применять уже критерий Стьюдента. Это свидетельствует об отсутствии у автора самых минимальных понятий о непараметрических критериях статистики, и об ограничениях, при которых используются параметрические методы сравнения. А между тем объект исследований у этого автора – дети в зоне радиактивного следа. По рекомендациям этого автора будут делаться выводы об их здоровье, изменяться методики лечения и т.д.

Если исходить из разумного предположения, что уровень профессиональной подготовки и квалификации авторов публикаций в среднем должен быть несколько выше уровня основной массы читателей, то, очевидно, сколь мало могут почерпнуть для себя читатели из подобных описаний. С другой стороны, авторы работ, диссертационные советы и редакции журналов, зная, что «...многие читатели медицинских журналов...не знакомы с основами медицинской статистики» [51], полагают, что и такой уровень описания не вызовет аргументированного протеста у потребителя такой некачественной информации. При чтении такого «новояза» возникает ощущение, что его целью является не детализация исследования, а попытка магией известных фамилий, статистической терминологией и наименованиями компьютеров придать работе более респектабельный и весомый вид, убедить коллег и читателей, диссертационный совет, экспертов ВАК, а возможно и самих себя, в статистической достоверности декларируемых научных выводов. Можно сказать, что подобные описания хорошо иллюстрируют известную фразу М.В. Ломоносова: «Смутно пишут о том, о чем смутно представляют».

Какие методы и критерии используются

Ниже приводится таблица 1 с частотой использования основных статистических параметров, методов и критериев в проанализированных нами статьях, монографиях и диссертациях.

Таблица 1.

Практика экспериментальных исследований вырабатывает определенные представления о способах обработки, которые де-факто становятся стандартными в соответствующих областях. Из данной таблицы можно сделать вывод о том, что такой стандарт стихийно сложился и для биомедицинской тематики. В том или ином объеме методы статистики применялись в 83% работ. При этом в 82% диссертаций, монографий и статей авторы приводили выборочные дескриптивные статистики в виде М±m. Однако только в 28 работах было дано объяснение этим выражениям примерно такого вида: «Все значения представлены в виде средней±стандартное отклонение» либо «Выборочные характеристики представлены в виде средней±ошибка средней». Однако в ряде публикаций встречаются и иные определения величины «m»: «Произведен расчет среднеарифметических значений (М), среднеквадратичных отклонений (s) и дисперсии средних значений (m)» – стр. 24 диссертации «Местные факторы защиты при острых заболеваниях органов мочевыделения у детей», 14.00.09 – педиатрия, 1994 г. Подавляющее же большинство авторов вообще никак не уточняет смысл выражения М±m. Между тем сравнение выражений М±m для одних и тех же переменных из различных работ иногда показывало, что если значения для «М» достаточно близки, то величины для «m» отличаются порой в 5...8 раз. Это позволяет предположить, что ряд авторов подразумевает под «m» стандартное (среднеквадратичное) отклонение SD (Standard Devation), тогда как другие – стандартную ошибку среднего: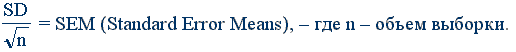

В пользу этого предположения говорит и тот факт, что для ряда переменных левая граница 95%-ного доверительного интервала для M, вычисленная с использованием m, принимала отрицательное значение, что противоречило смыслу этих переменных, средние значения которых по своей природе не могли быть нулевыми или отрицательными. Однако возможно, что такие значительные различия объяснялись и большой разницей объемов выборок, которые приводились не всегда. Опрос более 200 исследователей в области медицины и биологии о смысле выражения М±m показал, что значение М все опрошенные понимают как среднее. Примерно 50% опрошенных понимали под m среднеквадратичное отклонение SD, 40% – считали m стандартной ошибкой среднего (SEM) и 10% считали, что m – это полуширина доверительного интервала.

В 81% работ при описании результатов статистического анализа авторы использовали выражение «р <», обычно в виде «р < 0,05», «р < 0,01» или «р < 0,001». Наличие этого выражения означает, что авторы произвели проверку неких статистических гипотез – равенство генеральных средних, равенство коэффициентов корреляции, проверка адекватности уравнения регрессии и т.д. Однако для проверки одной и той же гипотезы могут быть использованы разные статистические критерии. Правильный выбор критерия определяется как спецификой данных и проверяемых гипотез, так и уровнем статистической подготовки исследователя. К сожалению, в каждом второй работе вообще отсутствует упоминание об использованных авторами статистических критериях проверки выдвигаемых гипотез. Между тем, эта информация имеет принципиальный характер для оценки истинности полученных результатов и степени доверия к ним.

Как видно из табл.1 в проанализированных работах доминируют методы, разработанные 50 и более лет тому назад [54...58]. Основная часть публикаций содержит сравнение контрольной группы объектов с опытными группами, которое в основном сводится только к проверке гипотезы о равенстве групповых средних с помощью t-критерия Стьюдента. При этом не производилась проверка исходной однородности контрольных и опытных групп до начала эксперимента. Между тем, вследствие такой неоднородности полученные выводы могут быть весьма сильно искажены, а в ряде случаев в пределах генеральной совокупности и вообще оказаться недостоверными.

В раздел «Прочие методы статистики» (8% работ) попали следующие методы и критерии: U-критерий Вилкоксона; критерий Манна-Уитни; критерий Колмогорова-Смирнова; пробит-анализ; точный критерий Фишера для анализа таблиц сопряженности; однофакторный дисперсионный анализ с множественными тестами сравнения Шеффе и Дункана; критерий Краскела-Валлиса; последовательный анализ Вальда; F-критерий Фишера; критерий T2-Хоттелинга, D-Махаланобиса, анализ таблиц выживаемости Мантеля-Кокса и Каплана-Майера, логистическая регрессия, модель пропорционального риска Кокса, arcsin-преобразование Фишера, спектральный анализ с быстрым преобразованием Фурье, ранговая корреляция Спирмена; метод максимального правдоподобия; дискриминантный анализ; кластерный анализ. Такое многообразие методов, сосредоточенное в 8% работ, говорит о том, что передовые исследователи уже не удовлетворяются дежурными методами типа t-Стьюдента. Но это же говорит и о том, что большинство из них встречается в публикациях весьма редко. В частности, некоторые из этих методов встречались в проанализированных нами публикациях по одному разу.

Сколько методов применяют в одной работе?

В 82% работ был применен 1 метод, 2 метода – 13%, 3 метода – 3,9% и 4 метода – 0,42%. Много это, или мало? Чтобы ответить на этот вопрос, попытаемся представить себе минимальный типовой набор методов, необходимых для выполнения статистического анализа кардиологических и радиобиологических данных. Для определения такого набора будем исходить из типичных ситуаций возникающих в ходе подобных исследований. Нередко, в практике подобных исследований, часть анализируемых показателей представляет собой качественные дискретные признаки. Например: депрессия сегмента ST на ЭКГ; наследственность пациента по тому или иному заболеванию, пол, тип производства, профессия и т.п. Обозначим эти показатели как множество Х. Другая часть показателей – это непрерывные количественные переменные: артериальное давление, диастолический или систолический объем, поглощенная доза излучения, возраст менархе и т.п. Эти переменные обозначим как множество Y. Тогда только для парных сочетаний признаков из двух разных множеств имеем следующие три комбинации: Х_i – Х_j; X_i – Y_j и Y_i – Y_j. Таким образом, если ограничиться только этими тремя минимально возможными комбинациями, то и тогда имеет смысл применить не менее 3 методов. Если же добавить к этому целесообразность исключения аномальных наблюдений, оценку основных выборочных параметров и проверку однородности сравниваемых групп, то это количество уже возрастает до 5...6 методов.

Отметим, что в 17% работ методы статистики не упоминались (читай: не использовались) вообще. В большей части это относится к статьям, нежели к диссертациям. В таких работах сообщается об изучении или сравнении двух или более групп пациентов, приводится количество пациентов, изучаемые показатели и т.д. Иными словами, речь идет о выборках, для изучения которых возможно применение тех или иных методов статистического анализа. Естественно, что отсутствие такого анализа снижает достоверность научных выводов приводимых в таких работах и делает их достаточно субъективными.

Коварный t-критерий Стьюдента

Наибольшей популярностью при проверке гипотез о равенстве генеральных средних (математических ожиданий) пользуется t-критерий Стьюдента. Частоты применения данного критерия в статьях разных журналов и диссертациях различных научных специальностях отличаются друг от друга незначительно. При чтении статей БЭБМ и «Вестника РАМН» складывается впечатление, что большинство авторов этих журналов знают и используют лишь t-критерий Стьюдента. Например, в 11-ти выпусках БЭБМ за 1997 г. t-критерий использован в 114 статьях, тогда как корреляционный и дисперсионный анализ применен всего лишь в 15 публикациях, критерий Колмогорова-Смирнова – в одной статье, парная линейная регрессия – в трех статьях, точный критерий Фишера – в трех статьях и т.д. В 56 статьях этих выпусков, в которых использовалось выражение «p < 0,05», авторы ничего не сообщили об использованных ими статистических критериях.

Критерий Стьюдента был разработан английским химиком У. Госсетом, когда он работал на пивоваренном заводе Гиннеса и по условиям контракта не имел права открытой публикации своих исследований. Поэтому публикации своих статей по t-критерию У. Госсет сделал в 1908 г. в журнале «Биометрика» под псевдонимом "Student", что в переводе означает «Студент». В отечественной же литературе принято писать «Стьюдент». Коварная простота вычисления t-критерия Стьюдента, а также его наличие в большинстве статистических пакетов и программ привели к широкому использованию этого критерия даже в тех условиях, когда применять его нельзя.

В период 1995...98 гг. мы провели опрос более 250 медиков и биологов, занятых научными исследованиями. Задавался следующий вопрос: «Каковы достаточные и необходимые условия использования t-критерия Стьюдента при сравнении групповых средних»? Ни один из опрашиваемых не смог полностью и правильно ответить на него. Примерно 50% говорили о нормальности распределения, однако не могли при этом объяснить, как реально проверить нормальность распределения. О втором необходимом условии никто из респондентов ничего не сказал.

Рассмотрим подробнее особенности использования t-критерия Стьюдента. Наиболее часто t-критерий используется в двух случаях. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящая из разных пациентов, количество которых в группах может быть различно. Во втором же случае используется так называемый парный t-критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, измеряется содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп. Из 1357 проанализированных статей, монографий, диссертаций и авторефератов, в которых авторы использовали t-критерий Стьюдента, упоминание о проверке нормальности распределения исследуемых признаков было только в 19 работах! Более того, лишь в единичных работах был проведен достаточно детальный анализ распределения вероятностей исследуемых количественных признаков, и на этом основании было принято аргументированное решение о выборе статистического критерия [67...68]. В подавляющем же большинстве работ авторы просто констатируют сам факт применения этого критерия, никак не касаясь проблем связанных с оценкой правомочности его использования.

Доминирование t-критерия Стьюдента в подавляющем большинстве диссертаций, монографий и статей отражает два важных аспекта. Во-первых, это свидетельство того, что авторы, использующие данный критерий, не имеют необходимых знаний относительно ограничений присущих данному критерию. Во-вторых, это говорит также и о том, что этим авторам неизвестны какие-либо альтернативы данному критерию, либо они не в состоянии ими самостоятельно воспользоваться. Можно без преувеличения сказать, что в настоящее время бездумное применение t-критерия Стьюдента в большинстве биомедицинских публикаций приносит больше вреда, нежели пользы.

Часть 6

Оглавление

Дата публикации:

15 августа 1999 года