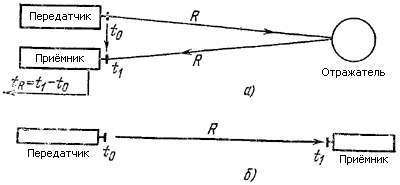
Задача 67-3. Многосигнальная локация

Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов

А.

Если по одному концу длинной стальной трубы стукнуть молотком, то на другом конце можно услышать этот звук. Можно ли по звуку определить длину трубы?

Б.

Вспоминая радиолокацию, т.е. наиболее распространенный метод измерения расстояний по времени прохождения сигналов, мы обнаруживаем следующие закономерности:

1. По отраженному сигналу (рис. 82, а) измерение дальности осуществляется просто: сигнал передатчика излучается в момент t₀ и, пройдя путь 2R (туда и обратно), возвращается в приемник в момент t₁. Сравнивая моменты t₁ и t₀, мы находим:

где v – скорость распространения сигнала. Отсюда находим:

R = vtR/2.

Рис. 82. Структурные схемы локаторов

Главной особенностью является наличие в приемнике информации как о моменте старта t₀ (поступает непосредственно из передатчика в приемник), так и о моменте финиша t₁ (поступает в виде отраженного сигнала). Разумеется, учитывают и задержку сигнала t₀ в цепях передатчика-приемника, либо делают общую антенну, тогда эту задержку можно сделать равной нулю.

2. По прямому сигналу (рис. 82, б) измерение R невозможно: в приемнике известен только момент приема t₁ и неизвестен момент передачи t₀. По прямому сигналу локация определяет обычно только па-правление на источник сигнала.

В нашей задаче с трубой передатчик (молоток) находится на одном конце измеряемого расстояния, приемник (ухо) – на другом. Следовательно, работа ведется по прямому сигналу, измерение длины трубы невозможно.

Однако измеряем же мы расстояние до молнии! Или до стреляющей пушки. На это возражают, что в таких измерениях используется свет и звук. Если бы мы видели взмах молотка в момент t₀ и приняли бы по трубе звук в момент t₁, то получили бы:

где ν – скорость звука.

Эти возражения справедливы: по условиям задачи надо обойтись только звуком.

Но одно неверно: формула (2). Если ее получить более корректно и затем проанализировать, вы догадаетесь и о том, как с помощью только звука определить длину трубы.

В.

В формуле (2) фигурируют два момента времени: t₁ и t₀. При более внимательном анализе обнаруживается, что определяющих задачу о пушке (молнии) моментов времени не два, а три:

а) момент выстрела t₀ (свет и звук);

б) момент прихода света к наблюдателю t₁;

в) момент прихода звука t₂.

Очевидны соотношения

где v₁ и v₂ – скорости распространения сигналов.

Момент t₀ нам неизвестен (зафиксировать его наблюдатель мог бы по сигналу, распространяющемуся мгновенно, но таких сигналов не бывает). Однако t₀ можно найти: ведь (3) и (4) есть система двух уравнений с двумя неизвестными R и t₀. Поскольку нас интересует только R, то t₀ просто можно исключить из рассмотрения. Вычитая, например, (3) из (4), имеем:

Итак, мы вывели точную формулу (5) взамен неточной (2). Правда, в случае молнии обе эти формулы практически совпадают, так как скорость света существенно больше скорости звука в воздухе:

v₀ = 300 000 км/с >> 0,33 км/с = v₂,

и поэтому слагаемым R/v₁ в (5) можно пренебречь. Однако тогда формула (5) теряет свою эвристическую силу. В точном же виде (5) легко подсказывает нам, как решить задачу. Если мы обязаны ограничиться только звуком, то, согласно формуле (5), надо изыскать два звука, распространяющихся вдоль трубы с различными скоростями.

Теперь сообразить уже легко: помимо звука, идущего по стальной трубе, необходимо принять звук, идущий по воздуху. Звук, идущий по наружному воздуху, ослабевает обратно пропорционально квадрату расстояния и поэтому для больших расстояний непригоден. Звук, идущий по воздуху, заполняющему трубу, почти не рассеивается в стороны и ослабевает только благодаря поглощению. Скорость продольных волн в стали v₁ = 5050 м/с; скорость звука в воздухе при температуре 0°C v₂ = 330 м/с (а вообще она пропорциональна корню квадратному из абсолютной температуры).

Поэтому, если tR = t₂ – t₁ = 2 с, то:

Итак, приняв два импульса звука и заметив моменты их прихода t₁ и t₂, мы измерим по формуле (5) длину трубы. Это локация по прямому сигналу. Как видим, по прямому сигналу тоже можно определить не только направление, но и дальность. Правда, при условии, что имеются два сигнала с различными скоростями распространения. Такую локацию будем называть двухсигнальной.

Заметим, что помимо двух ударов в моменты t₂ и t₁, мы еще будем все время, начиная с момента t₁, слышать в трубе смутный гул. Это следствие многих причин, две из которых мы назовем. Первая – распространение звука не только по прямой, но и по ломаным, например по воздуху, внутри трубы с многократными отражениями от стенок. Ломаная длиннее прямой, поэтому этот гул будет слышен после момента t₂. При падении звука из воздуха на стенку трубы отражается только часть звука, а остальное преломляется внутрь стали и после этого движется к нашему уху по стали с большей скоростью. Эта часть гула принимается между моментами t₁ и t₂. Вторая причина гула – отражение звука от конца трубы (это в основном касается волн, бегущих в стали). Добежав до конца трубы, звук отражается и бежит по стали назад, отражается от другого конца и т.д. Этот вид звука в нашем примере будет появляться на наблюдаемом конце трубы после момента t₁ с периодом:

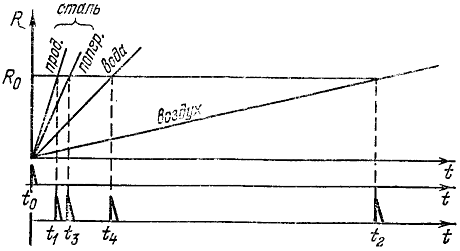
быстро ослабевая и маскируясь другими шумами (например, отражениями от неоднородностей, вызванные несовершенством сварных швов). Формула (7) является формулой локации для отраженного сигнала. По измеренному T она позволила бы длину трубы определить на том конце, на котором по ней ударяют молотком.

Еще пример двухсигнальной локации. По поверхности воды произведен удар, в другой точке водоема приняты два звуковых сигнала с интервалом tR = 1 с, Один из сигналов пришел по воде (ν₁ = 1500 м/с), второй – по воздуху. Согласно (6) R = 430 м.

Вернемся к трубе. Помимо продольных волн в стали возникают и поперечные, скорость которых ν₃ = 3300 м/с. А если горизонтальную трубу наполовину заполнить водой, то возникает еще и четвертый сигнал, распространяющийся со скоростью ν₄ = 1500 м/с. Система становится четырехсигнальной.

Рис. 83. Графики движения четырех сигналов

На рис. 83 показаны графики движения четырех сигналов вдоль трубы длиной R₀, удар сделан в момент T₀, на другом конце трубы сигналы приняты в моменты T₁, T₂, T₃ и T₄.

Дает ли это что-нибудь для измерения длины трубы? Ведь для отыскания двух неизвестных R и T₀ достаточно системы из двух уравнений.

В принципе это так, и если бы входящие в них ν₁, ν₂ и tR были абсолютно точны, то и дополнительные уравнения были бы лишними. В реальных условиях, поскольку всякая величина известна с ошибкой, то всякая избыточность информации полезна, так как позволяет уменьшить результирующую ошибку. По четырем каналам можно осуществить три независимых измерения R, после чего для уточнения взять хотя бы среднее арифметическое. При неравных точностях отдельных измерений слагаемые в «среднее арифметическое» подставляются не на равных правах, а с «весом» тем большим, чем точнее соответствующее измерение. Подробности – в теории статистических решений.

Точность отдельных измерений действительно неодинакова. Так, например, скорость звука в воздухе сильнее зависит от температуры и, кроме того, меняется вместе с ветром. К металлу ветер не имеет отношения. Кроме того, можно показать, что если два сигнала сильно разнятся по скорости (ν₁ >> ν₄, как например, на рис. 83), то относительная погрешность измерений определяется только относительной погрешностью меньшей из скоростей. Если же две скорости (ν₁ и ν₃ на рис. 83) мало отличаются друг от друга, требуется высокая точность знания обеих скоростей, что объясняется наличием их разности в знаменателе формулы (6).

Например, расстояние до молнии в принципе можно было бы вычислить не по сигналам свет–звук, а по сигналам свет–радио, так как молния сопровождается и радиоизлучением, причем скорость радиоволн в ионизированном воздухе грозы меньше скорости света. Однако это различие невелико и, кроме того, из-за изменчивости условий трудно предсказуемо. Поэтому точность определения расстояния была бы меньше, чем по сигналам свет – звук или радио – звук.

В ионизированной среде можно для измерений использовать и сигналы радио – радио (две различные волны), так как скорость оказывается зависящей от длины волны (для более длинных волн ν меньше). Это явление используется в радиоастрономии для измерения расстояний до пульсаров*.

* См., например, В.Л. Гинзбург, Пульсары, «Знание», 1970.

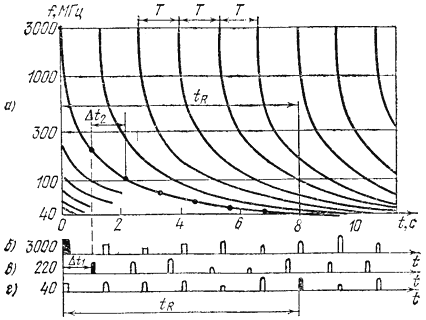
Рис. 84. Осциллограмма мерцания пульсара

Пульсар – нейтронная звезда, быстро вращающаяся. Его радиоизлучение достигает Земли в виде коротких импульсов, периодически повторяющихся в такт вращению. Первый из открытых пульсаров CP1919 имеет период следования импульсов T = 1,337 с. Эти импульсы принимаются на разных волнах. Наличие в межзвездной среде ионизированных частиц приводит к тому, что время пребывания в пути для некоторого импульса на волне 7,5 м (частота ≈ 40 МГц) на tR = 8 с больше (рис. 84), чем для того же импульса на волне 10 см (f = 3000 МГц). Это видно из того, что кривая, выходящая из левого верхнего угла (координаты: 3000 МГц и 0 с), пересекает ось абсцисс в точке t = 8 c. По известной концентрации электронов в межзвездной среде (в среднем 1 электрон в 30 см³) и по этому запаздыванию определено расстояние до пульсара:

R ≈ 410 св. лет ≈ 13 10⁹ св. с ≈ 3,9·1015 км.

Весьма поучительно, что полный путь от пульсара импульс проходит за 13·10⁹ с, а 8 с составляет менее одной миллиардной от полного пути. Столь малый эффект позволил, однако, сравнительно точно определить огромное расстояние, не определяемое пока никаким другим способом. Дальнейшие уточнения концентрации электронов позволят уточнить и оценку дальности.

В заключение рассмотрим одно затруднение, на которое вы, возможно, уже обратили внимание: как можно определить, что на двух волнах различие в запаздывании tR = 8 с, когда импульсы следуют с периодом T = 1,337 с? Ведь в задаче «Ломаная короче прямой» показано, что однозначно измеряются лишь запаздывания, не превосходящие периода следования импульсов tR < T. Действительно, это было бы невозможно, если бы пульсар не излучал и на промежуточных волнах. На рис. 84, а кривые показывают зависимость запаздывания каждого из импульсов от несущей частоты. На рис. 84, б показаны импульсы, принимаемые на частоте 3000 МГц, на рис. 84, г – на частоте 40 МГц. Зачернен один и тот же импульс. Сдвиг между зачерненными tR = 8 с, таков же сдвиг и в любой другой паре импульсов.

Отождествить зачерненные импульсы между собой (проще говоря, правильно их зачернить) можно, если использовать кривую в качестве путеводной нити, ведущей с частоты 3000 МГц на частоту 40 МГц. Для этого достаточно снять эту кривую, т.е. принимать импульсы не только на 3000 и 40 МГц, но и на всех промежуточных частотах (многосигнальная локация). Впрочем, не обязательно снимать всю кривую, достаточно снять ее на частотах, показанных жирными точками. Эти точки будут запаздывать друг относительно друга на Δt < T, и поэтому по двум соседним точкам запаздывание Δt измеряется однозначно. Так, например, на частоте 220 МГц (рис. 84, в) зачерненный импульс отстоит от соответствующего импульса на рис. 84, б на Δt₁ > T. Просуммировав все Δt, измеренные однозначно, мы получаем и однозначно измеренное tR:

tR = Δt₁ + Δt₂ + ... + Δt_N.

Поскольку в tR = 8 с укладывается T = 1,337 с примерно n = 6 раз, то для однозначных измерений tR необходимое число разных частот должно быть Ν ≥ n + 1 = 7, т.е. в этом случае локация должна быть, как минимум, семисигнальной. Правда, если бы теория могла гарантировать более точное предсказание формы кривой, то можно было бы обойтись и меньшим числом каналов. Положение, однако, обратное: кривую желательно снять экспериментально, располагая точки как можно гуще, чтобы такая экспериментальная кривая давала пищу теоретикам при решении других проблем.

• Задача 67. Два будильника

• Оглавление

Дата публикации:

26 июня 2004 года