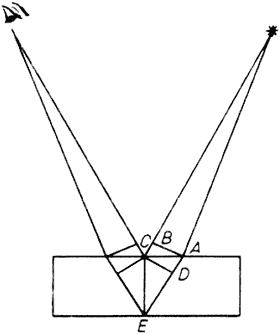
Существует ли эфир?

Виктор ЛАВРУС

О теории света и цветов

Томас ЮНГ

Хотя изобретение правдоподобных гипотез, независимых от каких-либо экспериментальных наблюдений, может принести очень мало пользы для развития естествознания, тем не менее открытие простых и единых принципов, с помощью которых большое число явно разнородных явлений сводятся к согласованным и универсальным законам, должно всегда считаться имеющим большое значение для усовершенствования человеческого разума; и чем больше и больше явлений оказываются согласующимися с принципами, заложенными в основу, тем более эти принципы могут претендовать на замену звания «гипотеза» званием «фундаментальный закон природы».

Цель сегодняшнего доклада не столько выдвижение каких-либо абсолютно новых мнений, сколько обращение к ряду предложенных ранее теорий и к их непосредственным создателям, чтобы подкрепить эти теории дополнительными доказательствами и применить эти теории к большому числу разнообразных фактов, которые раньше были погружены в темноту. В этой связи не было абсолютно никакой необходимости проводить хотя бы один новый опыт, поскольку набралось уже большое количество экспериментов в высшей степени превосходных, поскольку они должны были проводиться без малейшей приверженности их авторов к системе, с помощью которой они будут объяснены. Тем не менее здесь будет изложен ряд фактов, ранее не наблюдавшихся, с тем чтобы показать полное согласие упомянутой системы с разнообразными явлениями природы, которые с ней связаны. (...)

Гипотеза I. Вселенную наполняет светоносный эфир малой плотности и в высшей степени упругий. (...)

Гипотеза II. Волнообразные движения возбуждаются в этом эфире всякий раз, как тело становится светящимся.

Комментарий. Я использую термин «волнообразное движение» (undulation), отдавая ему предпочтение перед словом «колебание» (vibration), потому что колебание обычно понимается как движение, происходящее попеременно то вперед, то назад вследствие сложения импульса тела и ускоряющей силы, которое, естественно, более или менее непрерывно. Волнообразное же движение предполагается состоящим из колебательного движения, последовательно распространяющегося через различные части среды без всякого стремления каждой частицы продолжать свое движение, кроме как в связи с передачей следующих друг за другом волнообразных движений от явно колеблющегося тела. Так в воздухе вибрирующая струна создает волнообразные движения, представляющие звук. (...)

Гипотеза III. Ощущение различных цветов зависит от различной частоты колебаний, возбуждаемых светом в сетчатке. (...)

Предложение VIII. Когда два волнообразных движения от разных источников либо точно совпадают, либо очень близки по направлению, их общее действие состоит в комбинации движений, принадлежащих каждому из них.

Поскольку каждая частица среды подвержена действию каждого волнообразного движения, где бы ни совпадали их направления, волнообразные движения могут распространяться не иначе как объединяя свои движения, так что объединенное движение может быть либо суммой, либо разностью отдельных движений в соответствии с тем, сходные или несходные части волнообразных движений совпадают.

Я уже раньше настаивал на широком применении этого принципа к гармоникам (звука), однако далее выяснится, что он еще более полезен для объяснения явлений цветов. Волнообразные движения, которые теперь нужно сравнить, имеют равные частоты. Когда два ряда в некий момент времени точно совпадают, то очевидно, что общая скорость движений частицы должна быть наибольшей. Ясно также, что она должна быть наименьшей и, если волнообразные движения равны по силе, полностью исчезать, когда момент наибольшего прямого движения, принадлежащего одному волнообразному движению, совпадает с моментом наибольшего обратного движения, принадлежащего второму. В промежуточном состоянии объединенное волнообразное движение будет обладать промежуточной силой; однако то, по каким законам должна изменяться эта промежуточная сила, нельзя определить без дополнительных данных. Хорошо известно, что в области звука сходные причины вызывают явление, называемое биениями. Два ряда волнообразных движений почти равной величины попеременно то объединяются, то уничтожают друг друга в зависимости от того, когда они более или менее точно совпадают по времени совершения соответствующих движений.

Следствие I. О цветах бороздчатых поверхностей. Бойль, по-видимому, был первым, кто наблюдал цвета царапин на полированных поверхностях. Ньютон их не заметил. Мазеас и м-р Брум провели на эту тему несколько экспериментов, однако не получили каких-либо удовлетворительных выводов. Между тем все разнообразие этих цветов очень просто выводится из этого предложения.

Пусть в данной плоскости имеются две отражающие точки, очень близкие друг к другу, и пусть плоскость расположена так, что отраженное изображение светящегося предмета, видимое в ней, окажется совпадающим с этими точками. Тогда очевидно, что длины падающего и отраженного лучей, взятые вместе, равны по отношению к двум точкам, если считать эти лучи способными к отражению во всех направлениях. Пусть теперь одна из точек опустилась ниже данной плоскости; тогда полный путь света, отраженного от нее, будет удлинен на величину, которая равна понижению точки, умноженному на удвоенный косинус угла падения (рис. 1).

Рис. 1.

Теперь, если равные волнообразные движения данных размеров заставить отразиться от двух точек, расположенных достаточно близко для того, чтобы казаться глазу одной точкой, то если только эта линия равна половине ширины полного волнообразного движения то отражение от пониженной точки будет так интерферировать с отражением от фиксированной точки, что поступательное движение одного будет совпадать с возвратным движением другого и оба они будут уничтожены. Когда же эта линия равна полной ширине волнообразного движения, эффект будет удвоен; а когда она будет равна полутора ширинам, то движения снова уничтожатся, и так далее для значительного числа изменений. Если же отраженные волнообразные движения будут разных типов, то они будут действовать друг на друга по-разному в зависимости от их отношения к различным длинам той линии, которая является разностью их двух путей и которая может быть названа интервалом запаздывания.

Для того чтобы эффект был более ощутимым, ряд пар точек нужно объединить в две параллельные линии; если поместить несколько таких пар линий рядом друг с другом, то они облегчат наблюдение. Если одну такую линию заставить поворачиваться вокруг другой как вокруг оси, то понижение относительно данной плоскости будет равно синусу угла наклона; и поскольку глаз и светящийся объект остаются фиксированными, разность длин путей будет меняться как этот синус.

Наилучшими объектами для экспериментов являются превосходные микрометры м-ра Ковентри; наиболее удобны те из них, которые состоят из параллельных линий, проведенных на стекле на расстоянии одной пятисотой дюйма друг от друга. Каждая из этих линий при рассмотрении в микроскоп оказывается состоящей из двух или более тонких линий, в точности параллельных, расположенных на расстоянии, несколько большем, чем одна двадцатая расстояния между смежными линиями. Я расположил один из таких микрометров так, чтобы он отражал солнечный свет под углом 45°, и зафиксировал микрометр таким образом, что, когда он вращался вокруг одной из линий как вокруг оси, я мог измерять угловое движение, и я обнаружил, что наиболее яркий красный свет получается при наклоне в 10¼°, 20¾°, 32° и 45°, синусы которых относятся как числа 1, 2, 3 и 4.

При всех других углах, когда солнечный свет отражался от поверхности, этот цвет пропадал при изменении наклона и был одним и тем же при равных наклонах в любую сторону.

Этот эксперимент дает очень сильное подтверждение теории. Невозможно вывести никакое его объяснение из предлагавшихся до сих пор гипотез; и я уверен, что трудно будет изобрести какую-нибудь новую гипотезу, объясняющую его. Существует впечатляющая аналогия между разделением цветов и получением музыкальной ноты с помощью последовательных отражений от эквидистантных железных стержней, что, как я обнаружил, прекрасно согласуется с известной скоростью звука и расстояниями между поверхностями.

Не представляется невероятным, что цвета покровов некоторых насекомых и некоторых других естественных тел, дающих при различном освещении красивейшее разнообразие, могут иметь такое происхождение, а не получаться из тонких пластин. В некоторых случаях одна царапина или бороздка может создавать сходные эффекты из-за отражений от ее противоположных краев.

Следствие II. О цветах тонких пластин. Когда поток света падает на две параллельные преломляющие поверхности, частичные отражения точно совпадают по направлению; в этом случае интервал запаздывания, взятый между поверхностями, так относится к их пути, как удвоенный косинус угла преломления к единице. Так, рисуя АВ и CD перпендикулярно лучам (рис. 2), мы получаем, что времена прохождения ВС и AD равны, a DE будет составлять половину интервала запаздывания; но DE относится к CE как синус DCE к единице. Следовательно, для того чтобы DE оставалось постоянным или чтобы один и тот же цвет мог отражаться, толщина CE должна меняться как секанс угла преломления CED, что точно согласуется с экспериментами Ньютона, поскольку исправления, которые он ввел, совершенно незначительны.

Рис. 2.

Пусть среда между поверхностями будет более разреженной, чем окружающие среды. Тогда импульс, отраженный от второй поверхности, встречая последующее волнообразное движение на первой поверхности, будет придавать способность частицам более разреженной среды полностью останавливать движение более плотной и уничтожать отражение (предложение IV) в то время как они сами будут испытывать более сильное побуждение к движению, чем если бы они находились в покое, и количество прошедшего света будет увеличено. Таким образом, цвета, создаваемые отражением, будут уничтожаться, а цвета, создаваемые при прохождении, станут более яркими, когда удвоенная толщина, или интервал запаздывания, оказывается кратной полной ширине волнообразного движения, а при промежуточных толщинах эффект будет обратным в соответствии с наблюдениями Ньютона.

Если окажется, что такие же отношения хорошо выполняются по отношению к тонким пластинам более плотной среды, что, вообще говоря, не кажется невероятным, то необходимо будет принять исправленное доказательство Предложения IV. Однако в любом случае если тонкая пластина будет помещена между менее плотной и более плотной средами, то можно ожидать, что цвета, создаваемые при отражении и прохождении, поменяются местами.

Из ньютоновских измерений толщин, отражающих различные цвета, можно очень точно определить ширину и продолжительность соответствующих им волнообразных движений. Оказывается, что весь видимый спектр укладывается в отношение трех к пяти. Волнообразные движения красного, желтого и синего цветов должны быть связаны по величине как числа 8, 7 и 6, так что интервал от красного до голубого составляет одну четверть. (...)

Трактат о свете

в котором объяснены причины того, что с ним происходит при отражении и при преломлении, в частности при странном преломлении исландского кристалла

Христиан ГЮЙГЕНС

Предисловие

(...) Доказательства, приводимые в этом трактате, отнюдь не обладают той же достоверностью, как геометрические доказательства, и даже весьма сильно от них отличаются, так как в то время, как геометры доказывают свои предложения с помощью достоверных и неоспоримых принципов, в данном случае принципы подтверждаются при помощи получаемых из них выводов. Природа изучаемого вопроса не позволяет, чтобы это происходило иначе. Все же при этом можно достигнуть такой степени правдоподобия, которая часто вовсе не уступает полной очевидности. Это случается именно тогда, когда вещи, доказанные с помощью этих предполагаемых принципов, совершенно согласуются с явлениями, обнаруживаемыми на опыте, особенно когда таких опытов много и, что еще важнее, главным образом, когда открываются и предвидятся новые явления, вытекающие из применяемых гипотез, и оказывается, что успех опыта в этом отношении соответствует нашему ожиданию. Если в проведенном мной исследовании все эти доказательства правдоподобия имеются, а мне представляется, что дело как раз так и обстоит, то это должно служить весьма сильным подтверждением успеха моего исследования, и вряд ли положение вещей может значительно отличаться от того, каким я его изображаю. (...)

О лучах, распространяющихся прямолинейно

(...) Нельзя сомневаться в том, что свет состоит в движении какого-то вещества. Так, если обратить внимание на его происхождение, то оказывается, что здесь, на земле, его порождают главным образом огонь и пламя, которые, без сомнения, содержат в себе находящиеся в быстром движении тела. Это подтверждается тем, что огонь и пламя растворяют и плавят многие другие и даже самые твердые тела. Если рассмотреть действия, им производимые, то можно заметить, что когда свет собран вместе с помощью, например, вогнутых зеркал, он обладает свойством сжигать, как огонь, т.е. он разъединяет отдельные части тел. Последнее обстоятельство служит убедительным признаком движения, по крайней мере для истинной философии, в которой причину всех естественных явлений постигают при помощи соображений механического характера. По моему мнению, так и следует поступать, в противном случае приходится отказаться от всякой надежды когда-либо и что-нибудь понять в физике. (...)

(...) Как мною выше было сказано, звук делает в то же время за 1 секунду только 180 туазов, значит, скорость света более чем в 600 000 раз больше скорости звука. И все же это нечто совсем отличное от мгновенного распространения, так как разница здесь такая же, как между конечной вещью и бесконечной. Постепенное движение света оказывается, таким образом, подтвержденным, а отсюда следует, как я уже сказал, что это движение, так же как и звук, распространяется сферическими волнами.

Но если в этом отношении движения света и звука сходны, то во многих других отношениях они расходятся. Так, они различаются: начальным возбуждением причиняющего их движения, материей, в которой это движение распространяется, и способом, которым оно передается. В самом деле, известно, что возбуждение звука производится внезапным сотрясением всего тела или значительной его части, что возмущает весь смежный с ним воздух. Но движение света должно зарождаться от каждой точки светящегося тела; тогда, как это лучше выяснится из последующего, смогут быть видимы все отдельные части светящегося тела. И я думаю, что это движение может лучше всего послужить для объяснения, если предположить, что те из светящихся тел, которые, как пламя и, по-видимому Солнце и звезды, являются жидкими, состоят из плавающих в значительно более утонченной материи частиц. Эта материя приводит их в весьма быстрое движение и заставляет ударяться о частицы окружающего их эфира, причем эти последние значительно меньше первых. Что же касается твердых светящихся тел, как уголь или раскаленный на пламени металл, то у них рассматриваемое движение называется сильным сотрясением частиц металла или дерева, причем те частицы, которые находятся на поверхности, также ударяются о частицы эфирной материи. Впрочем, движение, возбуждающее свет, должно быть значительно более резким и быстрым, чем то, которое производит звук. Ведь мы не замечаем, чтобы содрогание звучащего тела могло произвести свет, точно так же как движением руки нельзя получить звук. (...)

(...) Ничто не мешает нам считать частицы эфира состоящими из материи, сколь угодно приближающейся к совершенной твердости и сколь угодно быстро восстанавливающей свою форму. Нам нет надобности исследовать для этого здесь причины этой твердости и упругости, так как рассмотрение их завлекло бы нас слишком далеко от нашего предмета. Я все же укажу здесь мимоходом, что частицы эфира, несмотря на их малость, можно себе представить состоящими еще из других частиц и что упругость их заключается в очень быстром движении тонкой материи, которая проходит сквозь них со всех сторон и заставляет их ткань располагаться так, чтобы она позволяла этой очень тонкой материи проходить через нее самым легким и свободным образом. Это согласуется с объяснением, которое дает упругости Декарт, но только я не предполагаю, как он, существования пор в форме полых круглых каналов. И не нужно думать, что в этом имеется что-нибудь нелепое или невозможное. Наоборот, представляется весьма вероятным, что природа как раз и пользуется этой бесконечной последовательностью частиц различных размеров, обладающих различной скоростью, чтобы производить такое множество удивительных явлений.

Но если бы даже мы не знали истинной причины упругости, все же мы постоянно видим, что этим свойством обладают многие тела; поэтому нет ничего странного в предположении, что им обладают также и весьма маленькие невидимые тела, как те, что составляют эфир. Если и желать найти какой-нибудь другой способ последовательной передачи движения света, то все же не отыщется такого, который бы лучше, чем упругость, согласовывался с равномерностью распространения движения, потому что если бы движение по мере удаления от источника света и распределения его по все большему количеству материи замедлялось, то на больших расстояниях оно не могло бы сохранить свою большую скорость. Если же предположить существование упругости у эфирной материи, то ее частицы будут обладать свойством восстанавливать свою форму одинаково быстро, независимо от того, будет ли воздействие на них сильным или слабым, и, таким образом, распространение света будет постоянно сохранять одну и ту же скорость. (...)

Следует подробнее рассмотреть происхождение этих волн и способ их распространения. Прежде всего из того, что было сказано о происхождении света, следует, что каждая маленькая часть какого-нибудь светящегося тела, как Солнце, свеча или раскаленный уголь, порождает свои собственные волны, центром которых она и является. Так, если в пламени свечи (рис. 3) отметить точки А, В и С, то концентрические круги, описанные около каждой из них, представят собой идущие от них волны. То же самое следует представить себе вокруг каждой точки как поверхности, так и внутренней части пламени.

Рис. 3.

Так как удары в центрах этих волн совершаются без определенной последовательности, то не нужно представлять себе, что сами волны следуют друг за другом на одинаковых расстояниях. Если на нашем рисунке эти расстояния показаны одинаковыми, то это скорее должно изображать передвижение одной и той же волны за одинаковые промежутки времени, чем несколько волн, исходящих из одного центра.

Впрочем, все это огромное количество волн, пересекающихся, не сливаясь и не уничтожая друг друга, отнюдь не являются непостижимым, раз известно, что одна и та же частица материи может служить для распространения нескольких волн, приходящих с разных и даже противоположных сторон, причем не только в том случае, когда ее толкают удары, близко следующие друг за другом, но даже и тогда, когда удары действуют на нее одновременно; основанием этого служит постепенное распространение движения.

Это может быть доказано на ряде одинаковых шаров из твердого вещества, о которых говорилось выше. Если одновременно ударить по ряду с двух противоположных концов равными шарами А и D (рис. 4), то каждый из них отскочит с той же скоростью, с какой он шел, а весь ряд останется на месте, хотя движение и прошло по всей длине его в том и другом направлениях. И если эти противоположно направленные движения встречаются в среднем шаре В или каком-либо другом шаре С, то соответствующий шар должен сжаться и выпрямиться в две стороны и, таким образом, в одно и то же мгновение послужить для передачи этих двух движений.

Рис. 4.

Сначала может показаться очень странным и даже невероятным, что волнообразное движение, производимое столь малыми движениями и тельцами, может распространяться на такие огромные расстояния, как, например, расстояние от Солнца или от звезд до нас. Действительно, сила этих волн должна ослабевать по мере их удаления от своего источника, так что каждая из них в отдельности, несомненно, теряет способность воздействовать на наше зрение. Но это перестает быть удивительным, если принять во внимание, что бесконечное число волн, исходящих, правда, из различных точек светящегося тела, на большом расстоянии от него соединяются для нашего ощущения только в одну волну, которая, следовательно, и должна обладать достаточной силой, чтобы быть воспринятой. Таким образом, то бесконечное число волн, которые одновременно нарождаются во всех точках неподвижной звезды, быть может, такой же большой, как и Солнце, для ощущения представляется только одной волной, которая вполне может быть достаточно сильной, чтобы вызвать впечатление в наших глазах. Кроме того, из каждой светящейся точки вследствие частых столкновений частиц, которые в этих точках ударяют в эфир, приходят многие тысячи волн в самое короткое время, которое только можно себе вообразить, а это делает их действие еще более чувствительным.

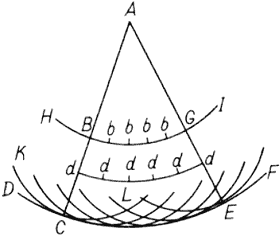
Рис. 5.

По поводу процесса образования этих волн следует еще отметить, что каждая частица вещества, в котором распространяется волна, должна сообщать свое движение не только ближайшей частице, лежащей на проведенной от светящейся точки прямой, но необходимо сообщает его также и всем другим частицам, которые касаются ее и препятствуют ее движению. Таким образом, вокруг каждой частицу должна образоваться волна, центром которой она является. Так, если DCF (рис. 5) – волна, исходящая из светящейся точки А, ее центра, то частица В, одна из тех, которые находятся в сфере DCF, производит свою отдельную волну KCL, которая коснется волны DCF в С в тот же момент, когда главная волна, исходящая из точки А, достигнет DCF. И ясно, что только точка С волны KCL, т.е. та, которая находится на прямой, проведенной через АВ, коснется волны DCF. Таким же образом остальные частицы, заключенные в сфере DCF, как bb, dd и т.д., создадут каждая свою волну. Но каждая из этих волн может быть только бесконечно слабой сравнительно с волной DCF, образованию которой содействуют все остальные волны той частью своей поверхности, которая наиболее удалена от центра А. (...)

Об отражении

Объяснив явление световых волн, распространяющихся в однородной среде, мы исследуем затем, что происходит с ними при встрече с другими телами. Сперва мы покажем, как этими же волнами объясняется отражение света и почему при нем сохраняется равенство углов. Пусть АВ (рис. 6) – плоская полированная поверхность какого-нибудь металла, стекла или другого тела, которую я сначала приму за совершенно гладкую (о неровностях, от которых она не может быть свободна, я скажу в конце этого доказательства), и пусть прямая AC, наклоненная к АВ, представляет собой часть световой волны, центр которой будет так далеко, что эта часть AC может быть принята за прямую линию. Я рассматриваю все это как бы в одной плоскости, представляя себе, что плоскость, в которой находится это изображение, пересекает сферу волны через ее центр, а плоскость АВ – под прямыми углами, о чем достаточно предупредить раз навсегда.

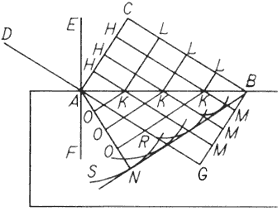
Рис. 6.

Точка С волны AC в некоторый промежуток времени продвинется до плоскости АВ к точке В по прямой СВ, которую должно представлять себе исходящей из светящегося центра и которая, следовательно, перпендикулярна AC. Но за тот же промежуток времени точка А той же волны не могла, по крайней мере отчасти, сообщить свое движение за пределы плоскости АВ и должна была продолжить свое движение в материи, находящейся над этой плоскостью, притом на протяжении, равном СВ; вместе с тем она должна была, согласно сказанному выше, образовать свою отдельную сферическую волну. Указанная волна изображена здесь окружностью NR, центр которой в А, а полудиаметр AN равен СВ.

Если затем рассмотреть остальные точки H волны AC, то ясно, что они не только достигнут поверхности АВ по прямым НК, параллельным СВ, но еще породят в прозрачной среде из центров К отдельные сферические волны, представленные окружностями, полудиаметры которых равны КМ, т.е. продолжениям линий H К до прямой BG, параллельной AC.

Но все эти окружности, как это легко видеть, имеют общей касательную прямую BN, т.е. ту же прямую, которая является касательной из точки В к первому из этих округов, центром которого была точка А, а полудиаметром, равным прямой ВС, AN.

Итак, прямая BN (заключенная между точками В и N, на которую падает перпендикуляр из точки А) как бы образована всеми этими окружностями и заканчивает движение, возникшее при отражении волны AC. Поэтому в этом месте движение имеется в гораздо большем количестве, чем где-либо, и, согласно объясненному выше, BN является распространением волны AC в тот момент, когда ее точка С достигла точки В. Действительно, нет другой прямой, которая, как BN, была бы общей касательной всех данных кругов, если не считать BG под плоскостью АВ. Эта BG была бы продолжением волны, если бы движение могло распространяться в среде, однородной с той, которая находится над плоскостью. Если мы хотим видеть, как волна AC постепенно достигла BN, то достаточно провести в той же фигуре прямые КО, параллельные BN, и прямые KL, параллельные AC. Тогда мы увидим, что волна AC из прямой последовательно становится ломаной во всех положениях OKL и снова становится прямой в NB.

Но отсюда видно, что угол отражения оказывается равным углу падения. Из того, что треугольники АСВ и BNA прямоугольны и имеют общую сторону АВ, а сторона СВ равна NA, следует, что углы, противолежащие этим сторонам, будут равны, а следовательно, также углы СВА и NAB. Но как СВ, перпендикулярная СА, показывает направление луча падающего, так AN, перпендикулярная волне BN, показывает направление луча отраженного; значит, эти лучи одинаково наклонны к плоскости АВ.(...)

О преломлении

(...) Для объяснения причины этих явлений, согласно нашим принципам, допустим, что прямая АВ (рис. 7) представляет собой плоскую поверхность, которой ограничены прозрачные тела, простирающиеся по направлению к С и N. Когда я говорю про плоскую поверхность, то имею в виду при этом не совершенно ровность, но такую же, какую мы принимали, когда рассматривали отражение, причем по тем же самым соображениям. Пусть линия AC представляет собой часть световой волны, центр которой, по предположению, так далек, что эту часть можно рассматривать как прямую линию. Тогда точка С волны AC в некоторый промежуток времени достигнет плоскости АВ по прямой СВ, которую нужно представлять себе исходящей из светящегося центра и которая, следовательно, пересечет AC под прямыми углами. Если бы материя прозрачного тела передавала движение волны так же быстро, как материя эфира, то за это же время точка А пришла бы в точку G по прямой AG, равной и параллельной СВ, и вся часть волны AC оказалась бы в GB. Но предположим, что она передает это движение менее быстро, скажем, на одну треть. Тогда от точки А движение распространится в материи прозрачного тела на расстояние, равное двум третям СВ, образовав свою отдельную сферическую волну, согласно сказанному выше. Эта волна изображена окружностью SNR, центр которой А, а полудиаметр равен двум третям СВ. Если рассматривать другие точки H волны AC, то окажется, что за то время, за которое точка С придет в В, они не только достигнут поверхности АВ по прямым НК, параллельным СВ, но сверх того произведут еще из центров К в прозрачной среде отдельные волны, представленные здесь окружностями, полудиаметры которых равны двум третям линий КМ, т.е. двум третям продолжений линий НК до прямой BG. Эти полудиаметры были бы равны целым КМ, если бы обе прозрачные среды были одинаковой проницаемости.

Рис. 7.

Следовательно, все эти окружности имеют общей касательной прямую линию BN, т.е. касательную из точки В к окружности SNR, которую мы рассматривали первой. Легко видеть, что все другие окружности коснутся той же линии BN от точки В до точки касания N, совпадающей с точкой, в которую падает AN, перпендикуляр к BN.

Таким образом, прямая BN, состоящая из ряда маленьких дуг этих окружностей, заканчивает движение, которое волна AC передала в прозрачное тело, и на этой прямой движение находится в большем количестве, чем где-либо в другом месте. И значит, эта прямая, согласно тому, что было сказано не раз, является распространением волны AC в тот момент, когда ее точка С достигла точки В. Действительно, под плоскостью АВ не существует другой линии, которая, как BN, была бы общей касательной всех указанных отдельных волн. Если хотят знать, каким образом волна AC постепенно достигла прямой BN, стоит только на том же рисунке провести прямые КО параллельно BN, а все KL – параллельно AC. Тогда будет видно, что волна СА из прямой становится ломаной последовательно во всех LKO, и снова становится прямой в BN. Это очевидно из того, что уже было показано, и не нуждается в дальнейших разъяснениях.

Если на том же рисунке провести прямую EAF (рис. 7), которая пересекла бы плоскость АВ под прямыми углами в точке А, и если линия AD будет перпендикулярна волне AC, то линия DA будет обозначать падающий луч света, а прямая AN, перпендикулярная BN, – луч преломленный: ведь лучи суть не что иное, как прямые линии, по которым распространяются части волн.

Отсюда ясно видно главное свойство преломления: именно синус угла DAE всегда находится в одном и том же отношении к синусу угла NAF, каким бы ни был наклон луча DA, и это отношение то же, что и отношение скорости волн в прозрачной среде, простирающейся в направлении АЕ, к скорости волн в прозрачной среде, простирающейся в направлении к AF. Действительно, если принять АВ за радиус круга, то синусом угла ВАС будет ВС, а синусом угла ABN будет AN. Но угол ВАС равен углу DAE, так как каждый из них, прибавленный к углу САЕ, образует прямой угол. Угол же ABN равен углу NAF, так как каждый из них образует прямой угол вместе с углом BAN. Следовательно, синус угла DAE относится к синусу угла NAF, как ВС к AN. Но отношение ВС к AN было равно отношению скоростей света в среде, простирающейся в направлении к АЕ, и в среде, простирающейся к AF. Таким образом, синус угла DAE относится к синусу угла NAF, как указанные скорости света. (...)

О своеобразном преломлении в исландском кристалле

1. Из Исландии, острова Северного моря, расположенного на широте 66°, привозят особого рода кристалл, или прозрачный камень, который весьма замечателен по своей форме и другим свойствам, но главным образом своими странными преломлениями света. Причины этих странных преломлений казались мне тем более достойными тщательного исследования, что среди прозрачных тел он один не следует обычным правилам по отношению к световым лучам. Я был даже до некоторой степени вынужден произвести эти исследования, так как преломления в этом кристалле, казалось, опровергали наше предшествующее объяснение правильного преломления. Но, как будет видно, данное нами объяснение, наоборот, весьма подтверждается этими преломлениями, если их свести к тому же принципу. (...)

18. Так как здесь имелись два различных преломления, я подумал, что существуют также и две различные категории распространяющихся волн света и что одна из них может существовать в эфирной материи, распространенной в теле кристалла. Эта материя, находясь в гораздо большем количестве, чем составляющие тело частицы, одна способна обусловить прозрачность согласно вышеприведенному объяснению. Я приписывал этой категории волн правильное преломление, наблюдаемое в этом камне, предполагая, что эти волны имеют обыкновенную сферическую форму и распространяются более медленно внутри кристалла, чем вне его; я показал, что от этого происходит преломление.

19. Что же касается другой категории, которая должна была произвести неправильное преломление, то я хотел испробовать, что будут давать эллиптические или, лучше сказать, сфероидальные волны. Я предполагал в соответствии с последним способом, которым я объяснял прозрачность, что эти волны будут распространяться одинаково как в эфирной материи, содержащейся в кристалле, так и в частицах, из которых он состоит. Мне казалось, что правильное расположение или размещение этих частиц могло способствовать образованию сфероидальных волн (для чего требовалось только, чтобы последовательное движение света распространялось немного быстрее в одном направлении, чем в другом), и я почти не сомневался в существовании в этом кристалле такого размещения равных и подобных частиц вследствие определенности и неизменности его формы и углов. Относительно этих частиц, их формы и расположения я предложу в конце этого трактата мои соображения и несколько подтверждающих их опытов. (...)

22. Допустив, таким образом, кроме сферических волн и подобные сфероидальные волны, я приступил к исследованию, могут ли они служить для объяснения явлений неправильного преломления и как с помощью этих явлений я мог бы определить форму и положение сфероидальных волн, в чем я достиг, наконец, желанного успеха. (...)

Неподвижен ли эфир или же он увлекается при движении тел?

Марио ЛЬОЦЦИ

Гипотеза упругих колебаний эфира сразу ставила проблему: неподвижен эфир или же движется? В частности, движется ли эфир, сконцентрированный в теле, вместе с этим телом? Прекрасные опыты Араго доказали, что движение Земли не оказывает никакого ощутимого воздействия на преломление света, приходящего от звезд.

Этот результат был несовместим с корпускулярной теорией, поэтому Араго обратился к Френелю с вопросом, укладывается ли он в рамки волновой теории. В одном из своих писем 1817 г. Френель ответил, что этот результат легко объясняется волновой теорией, как и явление аберрации, если только принять частичное увлечение эфира, т.е. принять, что движущееся тело увлекает с собой не весь содержащийся в нем эфир, а лишь избыточную часть эфира по сравнению с равным объемом пустого пространства. С помощью этой гипотезы Френелю удалось объяснить все явления, проистекающие из-за быстрого движения преломляющего тела.

Влияние движения тел, испускающих свет или звук, было исследовано теоретически в 1842 г. австрийским физиком Христианом Допплером (1803...1853), который показал, что при приближении источника света к наблюдателю период колебаний представляется наблюдателю меньшим, чем при неподвижном источнике, т.е. цвет излучения смещается в сторону ультрафиолета. Если же источник удаляется от наблюдателя, то цвет смещается в красную сторону спектра. Аналогично если источник звука приближается к наблюдателю, то звук воспринимается более высоким, а если удаляется – более низким; в этом явлении теперь легко убедиться, наблюдая изменение высоты звука гудка паровоза, проходящего мимо наблюдателя. В 1848 г. Физо предложил воспользоваться этим явлением, получившим название эффекта Допплера, или эффекта Допплера – Физо, для измерения радиальной составляющей скорости звезд по смещению их спектральных линий.

Уже сам Допплер заметил, что этот же метод можно применить для измерения скоростей двойных звезд; однако это измерение никому не удавалось провести, в том числе и Максвеллу. Применение допплеровского метода в астрофизике стало возможным лишь после появления в 1860 г. призмы прямого зрения, которую предложил астроном Джован Баттиста Амичи (1786...1863), известный конструктор оптических инструментов большой точности. Помимо этой призмы, как известно из учебников физики, он ввел в употребление еще другую призму (полного внутреннего отражения), названную в его честь, усовершенствовал микроскоп и предложил идею иммерсионного микроскопа. Призма прямого зрения Амичи состоит из призмы из флинтгласа, расположенной между двумя призмами из кронгласа; она дает спектр в направлении падающего луча.

В 1869 г. Фридриху Цолльнеру (1834...1882) пришла в голову счастливая идея применить пару противоположно расположенных призм прямого зрения Амичи, чтобы получить два противоположных спектра. Таким образом был создан так называемый реверсионный спектроскоп, который позволял уже использовать эффект Допплера. С этого момента значение эффекта Допплера в астрофизике чрезвычайно возросло.

Эффект Допплера тоже как будто подтверждал идею Френеля о частичном увлечении эфира; тем не менее эту гипотезу оспаривал Джордж Габриэль Стокс (1819...1903), один из наиболее блестящих продолжателей дела Френеля, известный прежде всего открытием в 1852 г. явления флюоресценции и закона, определяющего флюоресценцию, который и сейчас называется «законом Стокса». В известной работе, относящейся к 1845 г., Стокс отстаивает идею о полном увлечении эфира, находящегося в непосредственной близости от Земли, которое переходит постепенно в частичное увлечение, все более уменьшающееся по мере удаления от Земли.

В 1851 г. Физо пытался решить этот вопрос, заставив интерферировать два луча света, один из которых проходил столб воды в направлении ее течения, а второй – против течения. Если эфир увлекается при движении воды, то интерференционные полосы должны сместиться по отношению к тому положению, которое они занимают в опыте с неподвижной водой. Экспериментальные результаты, полученные Физо, подтвердили гипотезу Френеля. К тому же выводу привели исследования Эдуарда Кеттелера (1836...1900), проведенные в 1871 г., и исследования Майкельсона и Морли в 1886 г.

Но еще пятью годами раньше Майкельсон в своем ставшем впоследствии знаменитом опыте пытался экспериментально обнаружить движение Земли относительно эфира, принимаемого за неподвижный, т.е. обнаружить так называемый «эфирный ветер».

Примененный Майкельсоном метод можно назвать «методом двух путей»: один луч света, падая на слегка посеребренную пластину, расщеплялся на два взаимно перпендикулярных луча; эти лучи отражались по нормали от двух зеркал, расположенных на одинаковом расстоянии от пластины, возвращались обратно по тому же пути, сливались вместе и направлялись в оптическую систему. Если Земля движется относительно эфира, то из-за различия времен, требуемых для прохождения обоими лучами своих взаимно перпендикулярных путей, должна наблюдаться интерференционная картина. Хотя линейная скорость обращения Земли вокруг Солнца (30 км/сек) довольно мала по сравнению со скоростью света, экспериментальная установка была способна обнаружить даже в 100 раз меньший эффект. Этот опыт, многократно повторенный для различной ориентации прибора и в разное время года, давал у Майкельсона все время чисто отрицательный результат. Критика этого опыта со стороны Лоренца привела к тому, что Майкельсон вновь повторил его в 1887 г. вместе с Эдуардом Уильямом Морли (1838...1923) – и с тем же результатом. Таким образом, Майкельсон мог утверждать, что, согласно его опытам, эфир движется вместе с Землей. Однако явление аберрации света указывает на то, что эфир неподвижен. Эти два вывода резко противоположны один другому. В гл. 12 мы увидим, как это противоречие привело к появлению теории относительности.

Опыты Майкельсона были повторены с некоторыми усовершенствованиями Морли и Миллером в 1904 г. с тем же результатом. Позже, с 1921 по 1925 г., Миллер производил непрерывные наблюдения, которые привели его к выводу, что Земля движется по отношению к эфиру со скоростью 9 км/час. Однако этот вывод был опровергнут последующими опытами Джозефа Кеннеди и многими другими, вплоть до нового опыта Майкельсона, проведенного совместно с Пизом и Пирсоном в 1929 г.

Источники информации:

1. Дж. Бернал. Наука в истории общества – М., 1956.
2. Шухардин С.В. Документы по истории науки и техники – М., 1982.
3. Голин Г.М., Филонович С.Р. Классики физической науки (с древнейших времен до начала XX в.) – М.: Высш. Шк., 1989.
4. Марио Льоцци. История физики / Пер. с ит. Э.Л. Бурштейна – М.: Мир, 1970.
5. Веселовский И.Н. Христиан Гюйгенс. М., 1959.
6. Франкфурт У.И., Френк А.М. Христиан Гюйгенс. М., 1962.

См. также:

1. Лаврус В.С. Интеллект и изящество. НиТ, 1999.
2. Петров В.В. Опыт Майкельсона – Морли и гипотеза Френеля. НиТ, 2001.
3. Телегин М.Б. Бредли против Лоренца. НиТ, 2002.

Дата публикации:

30 ноября 1999 года